
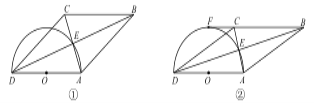
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
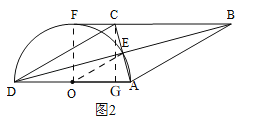
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先判断出四边形ABCD是平行四边形,再判断出AC⊥BD即可得出结论;
(2)先判断出AD=DC且DE⊥AC,∠ADE=∠CDE,进而得出∠CDA=30°,最后用弧长公式即可得出结论.
试题解析:证明:(1)∵四边形ABCD的对角线交于点E,且AE=EC,BE=ED,∴四边形ABCD是平行四边形.∵以AD为直径的半圆过点E,∴∠AED=90°,即有AC⊥BD,∴四边形ABCD 是菱形;
(2)由(1)知,四边形ABCD 是菱形,∴△ADC为等腰三角形,∴AD=DC且DE⊥AC,∠ADE=∠CDE.如图2,过点C作CG⊥AD,垂足为G,连接FO.∵BF切圆O于点F,∴OF⊥AD,且![]() ,易知,四边形CGOF为矩形,∴CG=OF=3.
,易知,四边形CGOF为矩形,∴CG=OF=3.
在Rt△CDG中,CD=AD=6,sin∠ADC=![]() =
=![]() ,∴∠CDA=30°,∴∠ADE=15°.
,∴∠CDA=30°,∴∠ADE=15°.
连接OE,则∠AOE=2×∠ADE=30°,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,如图所示,设点
,如图所示,设点![]() ,
,![]() ,
,![]() 所对应数的和是
所对应数的和是![]() .
.
⑴若以![]() 为原点,写出点
为原点,写出点![]() 所对应的数
所对应的数 ![]() 所对应的数 ,并计算
所对应的数 ,并计算![]() 的值是 :若以
的值是 :若以![]() 为原点,
为原点,![]() 又是 .
又是 .
(2)若原点![]() 在图中数轴上点
在图中数轴上点![]() 的右边,且
的右边,且![]() ,求
,求![]() .
.
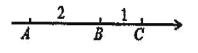
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为66万元;本周已售出2辆A型车和1辆B型车,销售额为42万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过84万元.问最多可以购买多少辆B型号的新能源汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
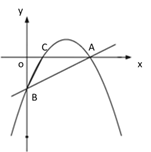
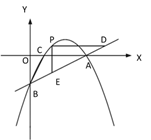
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
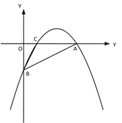
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
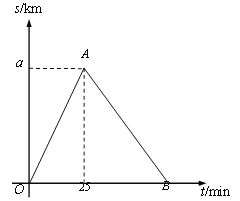
【题目】某市举行“迷你马拉松”长跑比赛,运动员从起点甲地出发,跑到乙地后,沿原路线再跑回点甲地.设该运动员离开起点甲地的路程s(km)与跑步时间t(min)之间的函数关系如图所示.已知该运动员从甲地跑到乙地时的平均速度是0.2 km/min,根据图像提供的信息,解答下列问题:
(1)a= km;
(2)组委会在距离起点甲地3km处设立一个拍摄点P,该运动员从第一次过P点到第二次过P点所用的时间为24min.
①求AB所在直线的函数表达式;
②该运动员跑完全程用时多少min?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是个三角形,分别连接这个三角形三边中点得到图2,再分别连接图2中间小三角形三边的中点得到图3.

![]() 图1中有_ __个三角形,图2中有 __个三角形,图3 中有 __个三角形;
图1中有_ __个三角形,图2中有 __个三角形,图3 中有 __个三角形;
![]() 按上面的方法继续下去,第
按上面的方法继续下去,第![]() 个图形有________个三角形;(用含
个图形有________个三角形;(用含![]() 的式子表示)
的式子表示)
![]() 当
当![]() 时,图形中有多少个三角形?
时,图形中有多少个三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简|a-3|+|a+2|;
(3)在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识准备:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() .则
.则![]() 两点之间的距离表示为:
两点之间的距离表示为:![]()
问题探究:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 且
且![]() 满足
满足![]()
![]() 直接写出:
直接写出:![]() ___、
___、![]()
![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,请问:当点
,请问:当点![]() 到
到![]() 两点的距离和为
两点的距离和为![]() 时,
时,![]() 满足什么条件?请利用数轴进行说明(此时
满足什么条件?请利用数轴进行说明(此时![]() 最小).
最小).
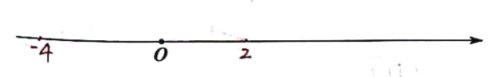
拓展:当数轴上 应用:国庆期间汉口江滩武汉关至长江二桥之间是观看“70周年国庆灯光秀”的理想区域,武汉关与长江二桥相距约![]() 三点对应的数分别为
三点对应的数分别为![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,当
,当![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?
的值最小? 
![]() 公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔
公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔![]() 公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作
公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作![]() 利用下图直接给出结果:
利用下图直接给出结果:![]() 满足的条件: 最小值为 公里.
满足的条件: 最小值为 公里.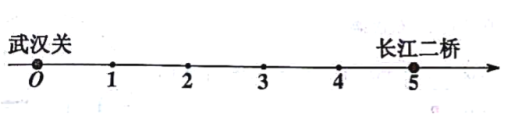
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com