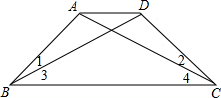
解:①AB=CD.利用如下:
∵∠1=∠2,∠3=∠4,
∴∠ABC=∠DCB,
在△ABC和△DCB中,
∠ABC=∠DCB,
BC=CB
∠4=∠3
∴△ABC≌△DCB,
∴AB=CD;
②△ACD与△ABE全等.理由如下:
∵∠BAC=∠EAD=90°,
∴∠BAE=∠CAD,
在△ACD和△ABE中,
AB=AC
∠BAE=∠CAD
AE=AD
∴△ACD≌△ABE.
分析:①由∠1=∠2,∠3=∠4得到∠ABC=∠DCB,加上BC=CB,∠4=∠3,根据全等三角形的判定可得到△ABC≌△DCB,根据全等三角形的性质即可得到AB=CD;
②由∠BAC=∠EAD=90°得到∠BAE=∠CAD,并且AB=AC,AE=AD,根据全等三角形的判定可得到△ACD≌△ABE.
点评:本题考查了全等三角形的性质与判定:有一条边对应相等,并且两组对应角相等的两三角形全等;有两边对应相等,并且它们所夹的角相等的两个三角形全等;全等三角形的对应边相等.

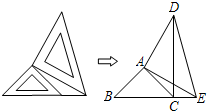


 =2,∠ADC=30°
=2,∠ADC=30°