解:
(1)在Rt△ABE中,
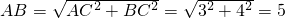
.
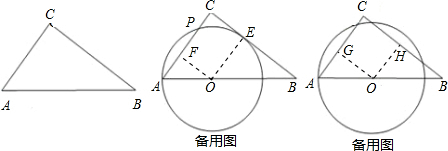
过点O作OD⊥BC于点D,则OD∥AC,
∴△ODB∽△ACB,∴
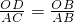
,∴
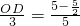
,∴
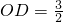
,
∴点O到BC的距离为

.
(2)证明:过点O作OE⊥BC于点E,OF⊥AC于点F,
∵△OEB∽△ACB,∴
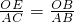
∴
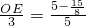
,∴
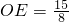
.
∴直线BC与⊙O相切.
此时,四边形OECF为矩形,
∴AF=AC-FC=3-

=

,
∵OF⊥AC,∴AP=2AF=

.
(3)
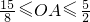
;
(4)过点O作OG⊥AC于点G,OH⊥BC于点H,
则四边形OGCH是矩形,且AP=2AG,
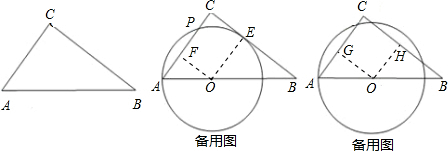
又∵CO平分∠ACB,∴OG=OH,∴矩形OGCH是正方形.
设正方形OGCH的边长为x,则AG=3-x,
∵OG∥BC,∵△AOG∽△ABC,
∴
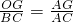
,∴
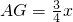
,
∴
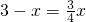
,∴
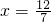
,∴AP=2AG=
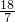
.
分析:(1)过点O作OD⊥BC于点D,易证△ODB∽△ACB,根据相似三角形的对应边的比相等即可求解;
(2)首先证明直线BC与⊙O相切,则四边形OECF为矩形,即可求得AF,进而求得AP的长;
(3)首先求得圆的半径,根据BC边与⊙O有公共点即直线与圆相切或相交,则圆心到直线的距离小于或等于圆的半径,即可求解;
(4)过点O作OG⊥AC于点G,OH⊥BC于点H,则四边形OGCH是矩形,矩形OGCH是正方形,设正方形OGCH的边长为x,则AG=3-x,易证
△AOG∽△ABC,根据相似三角形对应边的比相等即可求解.
点评:本题主要考查了相似三角形的判定与性质,并且与矩形、正方形的判定相结合,是一个综合性较强的题目.

 时,求点O到BC的距离;
时,求点O到BC的距离; 时,求证:直线BC与⊙O相切;此时线段AP的长是多少?
时,求证:直线BC与⊙O相切;此时线段AP的长是多少?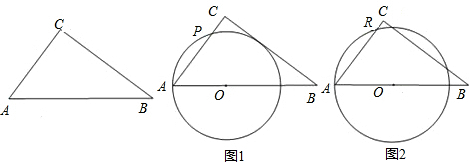

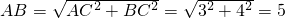 .
.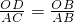 ,∴
,∴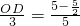 ,∴
,∴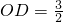 ,
, .
.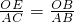 ∴
∴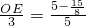 ,∴
,∴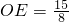 .
. =
= ,
, .
.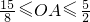 ;
;
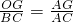 ,∴
,∴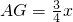 ,
,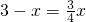 ,∴
,∴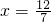 ,∴AP=2AG=
,∴AP=2AG=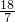 .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.