
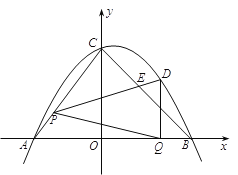
【题目】如图,在平面直角坐标系![]() 中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
中,已知A(-3,0),B(4,0),C(0,4). 二次函数的图像经过A、B、C三点.点P沿AC由点A处向点C运动,同时,点Q沿BO由点B处向点O运动,运动速度均为每秒1个单位长度.当一个点停止运动时,另一个点也随之停止运动.连接PQ,过点Q作QD⊥x轴,与二次函数的图像交于点D,连接PD,PD与BC交于点E. 设点P的运动时间为t秒(t>0).
⑴ 求二次函数的表达式;
⑵ 在点P、Q运动的过程中,当∠PQA+∠PDQ=90°时,求t的值;
⑶ 连接PB、BD、CD,试探究在点P,Q运动的过程中,是否存在某一时刻,使得四边形PBDC是平行四边形?若存在,请求出此时t的值与点E的坐标;若不存在,请说明理由.
【答案】⑴![]() ⑵当∠PQA = 90°-∠PDQ时,t的值为
⑵当∠PQA = 90°-∠PDQ时,t的值为![]() ⑶ 不存在某一时刻,使得四边形PBDC是平行四边形
⑶ 不存在某一时刻,使得四边形PBDC是平行四边形
【解析】(1)把A(-3,0),B(4,0),C(0,4)三点代入y=ax+bx+c即可求解;(2)求出直线AC的解析式,利用二次函数的解析式分别设出点P、D的坐标,作PH⊥DQ,可得DQ=2HQ,利用![]() 即可求出t的值;(3)由直线PD与BC相交于E,用含t的代数式设出点E的坐标,点E又在直线BC: y=-x+4上,得到关于t的一元二次方程,再利用根的判别式小于0,判断出方程无解即可.
即可求出t的值;(3)由直线PD与BC相交于E,用含t的代数式设出点E的坐标,点E又在直线BC: y=-x+4上,得到关于t的一元二次方程,再利用根的判别式小于0,判断出方程无解即可.
详解⑴设y=ax+bx+c,把A(-3,0),B(4,0),C(0,4)三点代入得
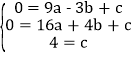 ,解得
,解得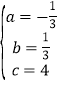
∴![]()
⑵![]() ,
,![]()
作![]() ,
,
∵![]() ∴
∴![]()
∴![]() =
=![]()
解得![]() (舍去),
(舍去),![]() ,
,
∴当∠PQA = 90°-∠PDQ时,![]() 的值为
的值为![]()
⑶不存在某一时刻,使得四边形PBDC是平行四边形.
理由:若四边形PBDC是平行四边形, 则BC平分线段PD,
![]()
∵点E又在直线BC: ![]() 上,
上,
∴![]()
![]()
整理得![]()
此方程根的判别式![]() ,
,
∴方程无实数根.
即不存在某一时刻,四边形PBDC是平行四边形.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年![]() 月的商品销售总额一共是
月的商品销售总额一共是![]() 万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
万元,如图(1)表示的是其中每个月销售总额的情况,图(2)表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图(1)、图(2),下列说法不正确的是( )
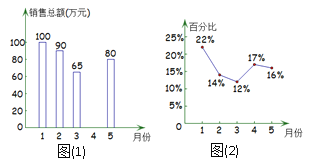
A. 4月份商场的商品销售总额是75万元 B. 1月份商场服装部的销售额是22万元
C. 5月份商场服装部的销售额比4月份减少了 D. 3月份商场服装部的销售额比2月份减少了
查看答案和解析>>
科目:初中数学 来源: 题型:
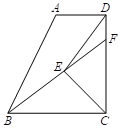
【题目】如图,在四边形ABCD中,∠ADC=∠BCD=90°,BC=CD=2AD,E为∠BCD平分线上的点,连接BE、DE, 延长BE交CD于点F.
⑴ 求证:△BCE≌△DCE;
⑵ 若DE∥AB,求证:FD=FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
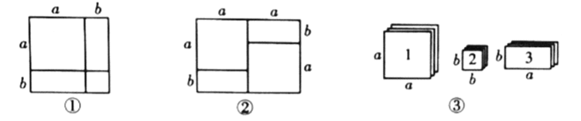
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
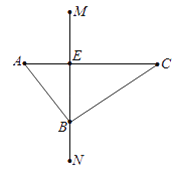
【题目】如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私A艇发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中错误的是( )
A. 有两角和其中一个角的对边对应相等的两个三角形全等
B. 有一边相等的两个等边三角形全等
C. 有两边和一角对应相等的两个三角形全等
D. 有两边和其中一边上的中线对应相等的两个三角形全等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com