解:去分母,将原方程两边同乘x(x-2),整理得2x
2-2x+(a+4)=0.①
方程①的根的情况有两种:
(1)方程①有两个相等的实数根,即△=4-4•2(a+4)=0.
解得a=-

.
当a=-

时,解方程2x
2-2x+(-

+4)=0,得x
1=x
2=

.
(2)方程①有两个不等的实数根,而其中一根使原方程分母为零,即方程①有一个根为0或2.
(i)当x=0时,代入①式得a+4=0,即a=-4.
当a=-4时,解方程2x
2-2x=0,x(x-1)=0,x
1=0或x
2=1.
而x
1=0是增根,即这时方程①的另一个根是x=1.它不使分母为零,确是原方程的唯一根.
(ii)当x=2时,代入①式,得2×4-2×2+(a+4)=0,即a=-8.
当a=-8时,解方程2x
2-2x-4=0,(x-2)(x+1)=0,x
1=2或x
2=-1.
而x
1=2是增根,即这时方程①的另一个根是x=-1.它不使分母为零,确是原方程的唯一根.
因此,若原分式方程只有一个实数根时,所求的a的值分别是-

,-4,-8,其对应的原方程的根依次为

,1,-1.
分析:先将原方程变形,转化为整式方程后得2x
2-2x+(a+4)=0①.由于原方程只有一个实数根,因此,方程①的根有两种情况:(1)方程①有两个相等的实数根,此二等根使x(x-2)≠0;(2)方程①有两个不等的实数根,而其中一根使x(x-2)=0,另外一根使x(x-2)≠0.针对每一种情况,分别求出a的值及对应的原方程的根.
点评:本题考查了分式方程的解法及增根问题.由于原分式方程去分母后,得到一个含有字母的一元二次方程,所以要分情况进行讨论.理解分式方程产生增根的原因及一元二次方程解的情况从而正确进行分类是解题的关键,本题属于竞赛题型,有一定难度.

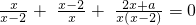 只有一个实数根,求a的值及对应的原方程的根.
只有一个实数根,求a的值及对应的原方程的根. .
. 时,解方程2x2-2x+(-
时,解方程2x2-2x+(- +4)=0,得x1=x2=
+4)=0,得x1=x2= .
. ,-4,-8,其对应的原方程的根依次为
,-4,-8,其对应的原方程的根依次为 ,1,-1.
,1,-1.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案