
| A. | $\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$ | B. | $\stackrel{→}{AB}$-$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | C. | $\stackrel{→}{AB}$+$\stackrel{→}{AD}$=$\stackrel{→}{BD}$ | D. | $\stackrel{→}{AB}$+$\stackrel{→}{BD}$=$\stackrel{→}{DA}$ |
分析 根据平面向量的平行四边形法则和三角形法则对各选项分析判断即可得解.
解答 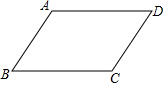 解:A、$\overrightarrow{AB}$与$\overrightarrow{CD}$的模相等,但是方向相反,则$\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$,故本选项正确;
解:A、$\overrightarrow{AB}$与$\overrightarrow{CD}$的模相等,但是方向相反,则$\stackrel{→}{AB}$+$\stackrel{→}{CD}$=$\stackrel{→}{0}$,故本选项正确;
B、$\overrightarrow{AD}$-$\stackrel{→}{AB}$=$\stackrel{→}{BD}$,故本选项错误;
C、$\overrightarrow{AD}$-$\stackrel{→}{AB}$=$\stackrel{→}{BD}$,故本选项错误;
D、$\overrightarrow{AB}$+$\overrightarrow{DA}$=$\overrightarrow{BD}$,故本选项错误;
故选:A.
点评 本题考查了平面向量,此类题目主要利用了平行四边形法则和三角形法则,要注意$\overrightarrow{0}$与0的不同.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
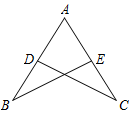 如图,点D、E分别在线段AB、AC上,联结BE,CD,BE=CD,要使△ABE≌△ACD,还需添加一个条件,这个条件可以是∠B=∠C(答案不唯一) (只要写一个条件).
如图,点D、E分别在线段AB、AC上,联结BE,CD,BE=CD,要使△ABE≌△ACD,还需添加一个条件,这个条件可以是∠B=∠C(答案不唯一) (只要写一个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
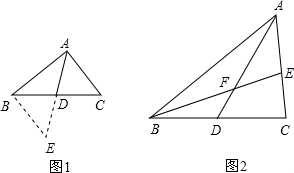 某校数学课外兴趣小组活动时,老师提出如下问题:
某校数学课外兴趣小组活动时,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com