
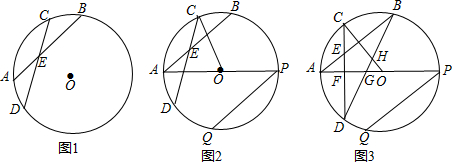
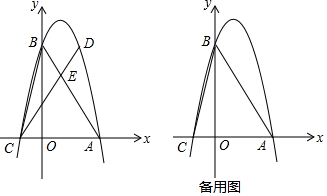
分析 (1)连接AD、BC,只要证明△AED≌△CEB,即可解决问题.
(2)连接AC.想办法证明:∠OCD、∠APQ都与∠PAB相等即可.
(3)连接AD、AH、BP、BQ、DP,延长CO交PQ于M,作AN⊥BD于N.由△COF≌△POM,推出M是PQ的中点,OC垂直平分AB,设GH=a,则BH=5GH=5a,由OC垂直平分AB,推出AH=BH=5a,∠HAB=∠HBA,推出∠AHD=2∠ABH,由$\widehat{AC}$=$\widehat{AD}$=$\widehat{BC}$,推出∠ADC=∠CDB=∠ABD,推出∠ADH=2∠ADC=2∠ABH=∠AHD,推出AH=AD=5a,由△ADF≌△GDF,推出AD=DG=5a,推出DH=6a,BD=11a,由AH=AD,AN⊥DH,推出NH=$\frac{1}{2}$DH=3a,AN=$\sqrt{A{H}^{2}-N{H}^{2}}$=4a,BN=BH+NH=8a,在Rt△ABN中,
tan∠ABD=$\frac{AN}{BN}$=$\frac{4a}{8a}$=$\frac{1}{2}$,由$\widehat{AD}$=$\widehat{AD}$,推出∠ABD=∠APD,推出tan∠ABD=tan∠APD=$\frac{1}{2}$,推出$\frac{AD}{PD}$=$\frac{1}{2}$,推出PD=2AD=10a,AP=$\sqrt{A{D}^{2}+P{D}^{2}}$=5$\sqrt{5}$a,再证明BQ为⊙O的直径,想办法列出方程即可解决问题.
解答 (1)证明:连接AD、BC,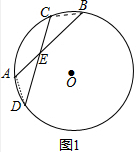
∵$\widehat{AC}$=$\widehat{AC}$,
∴∠B=∠D,
在△AED和△CEB中,
$\left\{\begin{array}{l}{∠D=∠B}\\{DE=BE}\\{∠AED=∠BEC}\end{array}\right.$,
∴△AED≌△CEB,
∴AD=BC,
∴$\widehat{AD}$=$\widehat{BC}$.
(2)证明:连接AC.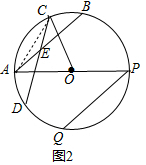
∵$\widehat{AD}$=$\widehat{BC}$,
∴∠BAC=∠ACD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAO=∠OCD,
∵PQ∥AB,
∴∠BAO=∠APQ,
∴∠COD=∠APQ.
(3)连接AD、AH、BP、BQ、DP,延长CO交PQ于M,作AN⊥BD于N.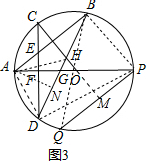
∵∠OCD=∠APQ.OC=OP,∠AOC=∠POM,
∴△COF≌△POM,
∴CF=PM,
∵PQ=2CF,
∴PQ=2PM,
∴M是PQ的中点,
∴OM⊥PQ,
∴∠CFO=∠PMO=90°
∴AP⊥CD,
∴$\widehat{AC}$=$\widehat{AD}$,
PQ∥AB,
∴∠OMP=∠AKM=90°,
∴OC⊥AB,
∴$\widehat{AC}$=$\widehat{BC}$,
∴AK=BK,
∴$\widehat{AC}$=$\widehat{AD}$=$\widehat{BC}$,OC垂直平分AB,设GH=a,
∴BH=5GH=5a,
∵OC垂直平分AB,
∴AH=BH=5a,∠HAB=∠HBA,
∴∠AHD=2∠ABH,
∵$\widehat{AC}$=$\widehat{AD}$=$\widehat{BC}$,
∴∠ADC=∠CDB=∠ABD,
∴∠ADH=2∠ADC=2∠ABH=∠AHD,
∴AH=AD=5a,
∵CD⊥AP,
∴∠AFD=∠GFD=90°,
∵DF=DF,∠ADC=∠CDB,
∴△ADF≌△GDF,
∴AD=DG=5a,
∴DH=6a,BD=11a,
∵AH=AD,AN⊥DH,
∴NH=$\frac{1}{2}$DH=3a,
AN=$\sqrt{A{H}^{2}-N{H}^{2}}$=4a,BN=BH+NH=8a,
在Rt△ABN中,
tan∠ABD=$\frac{AN}{BN}$=$\frac{4a}{8a}$=$\frac{1}{2}$,
∵$\widehat{AD}$=$\widehat{AD}$,
∴∠ABD=∠APD,
∴tan∠ABD=tan∠APD=$\frac{1}{2}$,
∵AP是直径,
∴∠ADP=90°,
∴$\frac{AD}{PD}$=$\frac{1}{2}$,
∴PD=2AD=10a,AP=$\sqrt{A{D}^{2}+P{D}^{2}}$=5$\sqrt{5}$a,
∵AP为直径,
∴∠ABP=90°,
∵PQ∥AB,
∴∠ABP+∠BPQ=180°,
∵∠ABP=90°,
∴∠BPQ=90°,
∴BQ为⊙O的直径,
∴BQ=5$\sqrt{5}$a,
∵BQ为⊙O的直径,
∴∠BDQ=90°,
∴DQ=$\sqrt{B{Q}^{2}-B{D}^{2}}$=2a,
∵DQ=4,
∴2a=4,
∴a=2,AP=5$\sqrt{5}$a=10$\sqrt{5}$,
∴⊙O的半径OA=$\frac{1}{2}$AP=5$\sqrt{5}$.
点评 本题考查圆综合题、平行线的性质、全等三角形的判定和性质、勾股定理、垂径定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用此时构建方程解决问题,题目比较难,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
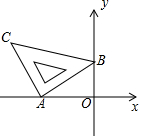 含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.
含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
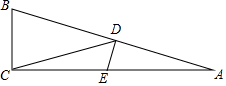 如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.
如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
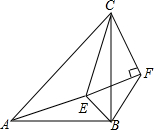 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com