
分析 (1)将已知等式相加后两两相消可得;
(2)根据$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$裂项相消可得;
(3)根据$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$裂项相消可得.
解答 解:(1)原式=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$=1-$\frac{1}{5}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$;
(2)原式=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$,
故答案为:$\frac{2016}{2017}$;
(3)原式=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)+$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$)+$\frac{1}{2}$($\frac{1}{9}$-$\frac{1}{11}$)
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{9}$+$\frac{1}{9}$-$\frac{1}{11}$)
=$\frac{1}{2}$×(1-$\frac{1}{11}$)
=$\frac{1}{2}$×$\frac{10}{11}$
=$\frac{5}{11}$.
点评 本题主要考查数字的变化规律,根据题意掌握裂项相消的方法是解题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
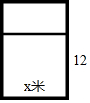 有12米长的木条,要做成一个如图的窗框,如果假设窗框横档的长度为x米,那么窗框的面积是(木条的宽度忽略不计)( )
有12米长的木条,要做成一个如图的窗框,如果假设窗框横档的长度为x米,那么窗框的面积是(木条的宽度忽略不计)( )| A. | x(6-$\frac{3}{2}$x)米2 | B. | x(12-x)米2 | C. | x(6-3x)米2 | D. | x(6-x)米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
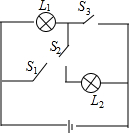 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com