
【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
【答案】
(1)300
(2)60,90
(3)72°
(4)解:从该校学生中随机抽取一个最关注热词D的学生的概率是 ![]() =
= ![]() .
.
答:从该校学生中随机抽取一个最关注热词D的学生的概率是 ![]()
【解析】解:(1)105÷35%=300(人).
(2)n=300×30%=90(人),m=300﹣105﹣90﹣45=60(人).
(3)![]() ×360°=72°.
×360°=72°.
(4)解:从该校学生中随机抽取一个最关注热词D的学生的概率是 ![]() =
=![]() .
.
答:从该校学生中随机抽取一个最关注热词D的学生的概率是 ![]()
故答案为:(1)300;(2)60,90;(3) 72°;(4)![]() .
.
(1)依据统计图可知A的人数为105人,所占的百分比为35%,最后,依据总数=频数÷百分比求解即可;
(2)C所对应的人数为:总人数×30%,B所对应的人数为:总人数-A所对应的人数-C所对应的人数-D所对应的人数,即可解答;
(3)依据圆心角=百分比×360°求解即可;
(4)用关键热词为D的人数除总人数即可.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E,F分别为BC,CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值
查看答案和解析>>
科目:初中数学 来源: 题型:
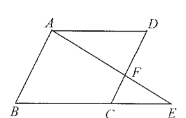
【题目】已知:如图,AD∥BE,∠B=∠D,直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由)。
解:直线AB与DC平行.理由如下:
∵ AD∥BE (已知 )
∴ ∠D = ∠DCE ( )
又∵∠B = ∠D ( )
∴∠B = ∠_____ (等量代换)
∴ AB∥DC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 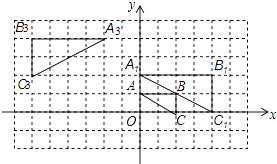
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题“已知![]() 且
且![]() ,
,![]() ,试确定
,试确定![]() 的取值范围”有如下解法:
的取值范围”有如下解法:
解:![]()
![]()
又![]()
![]()
![]() 又
又![]()
![]() ①
①
同理得:![]() ②
②
![]() 即
即![]() ,
,
请按照上述方法,完成下列问题:
(1)已知关于![]() 、
、![]() 的方程组
的方程组![]() 的解均为负数,若
的解均为负数,若![]() 且
且![]() ,求
,求![]() 的取值范围.
的取值范围.
(2)已知![]() ,
,![]() ,若
,若![]() 成立,求
成立,求![]() 的取值范围(结果用含
的取值范围(结果用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣ ![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2 , 求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com