
如图,一次函数y=x+b的图象与反比例函数y= (x>0)的图象交于点A(2,1),与x轴交于点B.
(x>0)的图象交于点A(2,1),与x轴交于点B.
(1)求k和b的值;
(2)连接OA,求△AOB的面积.
科目:初中数学 来源: 题型:解答题
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
下表中,y是x的一次函数.
| x |  2 2 | 1 | 2 | | 5 |
| y | 6 |  3 3 | |  12 12 |  15 15 |
 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
无论k取任何实数,对于直线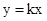 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线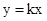 恒过定点
恒过定点 .
.
(1)无论 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了抓住世界杯商机,某商店决定购进A、B两种世界杯纪念品.若购进A种纪念品10件,B种纪念品5件,需要1 000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:关于x的一元二次方程mx2﹣(4m+1)x+3m+3="0" (m>1).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=x1﹣3x2,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于m的函数y=2m+b的图象与此图象有两个公共点时,b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com