
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.
(1)请直接写出点(2,2)的“关联点”的坐标;
(2)如果点P在函数y=x﹣1的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=x2的图象上,当0≤m≤2时,求线段MN的最大值.
【答案】(1)(2,0);(2)(2,1);(3)当0≤m≤2时,线段MN的最大值为6.
【解析】
(1)根据“关联点”的定义结合点的坐标即可得出结论;
(2)根据点P在函数y=x﹣1的图象上,即可得出P(x,x﹣1)、Q(x,1),再根据点P、Q重合即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据“关联点”的定义找出点N的坐标,分m≥n和m<n两种情况考虑,根据点N在函数y=x2的图象上,即可用含m的代数式表示出n,再根据两点间的距离公式即可找出MN的关系式,利用一次(二次)函数的性质即可求出线段MN的最大值.
解:(1)∵|2﹣2|=0,
∴点(2,2)的“关联点”的坐标为(2,0).
(2)∵点P在函数y=x﹣1的图象上,
∴P(x,x﹣1),则点Q的坐标为(x,1),
∵点Q与点P重合,
∴x﹣1=1,解得:x=2,
∴点P的坐标为(2,1).
(3)∵点M(m,n),
∴点N(m,|m﹣n|).
∵点N在函数y=x2的图象上,
∴|m﹣n|=m2.
(i)当m≥n时,m﹣n=m2,
∴n=﹣m2+m,
∴M(m,﹣m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM﹣yN|=|﹣m2+m﹣m2|=m|2m﹣1|.
①当0≤m≤![]() 时,MN=﹣2m2+m=﹣2(m﹣
时,MN=﹣2m2+m=﹣2(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,MN取最大值,最大值为
时,MN取最大值,最大值为![]() .
.
②当![]() <m≤2时,MN=2m2﹣m=2(m﹣
<m≤2时,MN=2m2﹣m=2(m﹣![]() )2+
)2+![]() ,
,
当m=2时,MN取最大值,最大值为6.
(ii)当m<n时,n﹣m=m2,
∴n=m2+m,
∴M(m,m2+m),N(m,m2).
∵0≤m≤2,
∴MN=|yM﹣yN|=|m2+m﹣m2|=m,
当m=2时,MN取最大值2.
综上所述:当0≤m≤2时,线段MN的最大值为6.


科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
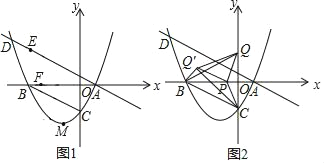
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
(1)求△ABC的面积;
(2)已知点M是抛物线的顶点,在直线AD上有一动点E,x轴上有一动点F,当ME+BE最小时,求|CF﹣EF|的最大值及此时点F的坐标;
(3)如图2,在y轴正半轴上取点Q,使得CB=CQ,点P是x轴上一动点,连接PC,将△CPQ沿PC折叠至△CPQ′.连接BQ,BQ′,QQ′,当△BQQ′为等腰三角形时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() ;其中正确的结论是( )
;其中正确的结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
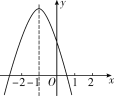
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
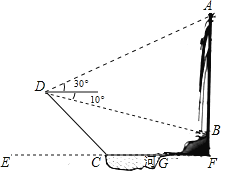
【题目】如图,为测量瀑布AB的高度,测量人员在瀑布对面山上的D点处测得瀑布顶端A点的仰角是![]() ,测得瀑布底端B点的俯角是
,测得瀑布底端B点的俯角是![]() ,AB与水平面垂直
,AB与水平面垂直![]() 又在瀑布下的水平面测得
又在瀑布下的水平面测得![]() ,
,![]() 注:C、G、F三点在同一直线上,
注:C、G、F三点在同一直线上,![]() 于点
于点![]() ,斜坡
,斜坡![]() ,坡角
,坡角![]() (参考数据:
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
![]() 求测量点D距瀑布AB的距离
求测量点D距瀑布AB的距离![]() 精确到
精确到![]() ;
;
![]() 求瀑布AB的高度
求瀑布AB的高度![]() 精确到
精确到![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°

(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款新产品,通过市场调研后,按三种颜色受欢迎的程度分别对A颜色、B颜色、C颜色的产品在成本的基础上分别加价40%,50%,60%出售(三种颜色产品的成本一样),经过一个季度的经营后,发现C颜色产品的销量占总销量的40%,三种颜色产品的总利润率为51.5%,第二个季度,公司决定对A产品进行升级,升级后A产品的成本提高了25%,其销量提高了60%,利润率为原来的两倍;B产品的销量提高到与升级后的A产品的销量一样,C产品的销量比第一季度提高了50%,则第二个季度的总利润率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com