
����Ŀ��ij������������·��֧���![]() ��˿���
��˿���![]() �ĺ�����ϵ��ͼ��ʾ����֧���
�ĺ�����ϵ��ͼ��ʾ����֧���![]() ��Ʊ����
��Ʊ����![]() ֧�����ã�������Ŀǰ������·���𣬹�˾�й���Ա������������飺����(��)���ı�֧�����ã���߳�Ʊ�۸���(��)���ı䳵Ʊ�۸���֧������. ����������ĸ�ͼ���У�ʵ�ߺ����߷ֱ��ʾĿǰ�ͽ����ĺ�����ϵ������ ��
֧�����ã�������Ŀǰ������·���𣬹�˾�й���Ա������������飺����(��)���ı�֧�����ã���߳�Ʊ�۸���(��)���ı䳵Ʊ�۸���֧������. ����������ĸ�ͼ���У�ʵ�ߺ����߷ֱ��ʾĿǰ�ͽ����ĺ�����ϵ������ ��

�� �� �� ��
A. �ٷ�ӳ�˽��飨���۷�ӳ�˽��飨�� B. �ڷ�ӳ�˽��飨��)���ܷ�ӳ�˽��飨��
C. �ٷ�ӳ�˽��飨���۷�ӳ�˽��飨�� D. �ڷ�ӳ�˽��飨���ܷ�ӳ�˽��飨��
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
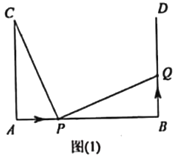
����Ŀ����ͼ(1)![]() ��
��![]() ��BD��AB��
��BD��AB��![]() ����
����![]() ���߶�
���߶�![]() ����
����![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶���ͬʱ����
�˶���ͬʱ����![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ���
���![]() �˶��������˶���ʱ��Ϊ
�˶��������˶���ʱ��Ϊ![]() .
.
(1)����![]() ���ٶ����
���ٶ����![]() ���ٶ���ȣ���
���ٶ���ȣ���![]() ʱ����֤��
ʱ����֤��![]() ��
��
(2)��(1)�������£��жϴ�ʱ![]() ��
��![]() ��λ�ù�ϵ����֤����
��λ�ù�ϵ����֤����
(3)��ͼ(1)�е���![]() ��
��![]() ��������
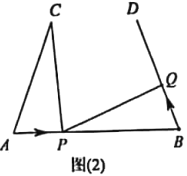
������Ϊ��![]() �����õ�ͼ(2)��������������.���
�����õ�ͼ(2)��������������.���![]() ���˶��ٶ�Ϊ
���˶��ٶ�Ϊ![]() �������Ƿ����ʵ��
�������Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ȫ�ȣ������ڣ������Ӧ��
ȫ�ȣ������ڣ������Ӧ��![]() ��
��![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������й�����˾�ƻ�����A�ͺ�B�����ֻ������ܹ�������10����������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1������A�ͺ�B������ÿ�����������Ԫ��
��2��Ԥ����ij��·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴Σ����ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ���������
��3���ڣ�2���������£����ֹ��������ܷ������٣������ܷ����Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����xһԪ���η���x2-2(k+1)x+k2-2k-3=0����������ȵ�ʵ����
��1����kȡֵ��Χ��
��2����k��С������ʱ���������� y= x2-2(k+1)x+k2-2k-3�Ķ��������Լ�����x��Ľ������ꣻ
��3������2������õ���������x���·��IJ�����x�ᷭ�۵�x���Ϸ���ͼ������ಿ�ֲ��䣬�õ�һ����ͼ�����㻭�������ͼ�������ͼ����ֱ�� y=x+m��������ͬ������ʱmֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ҽ�����ֲ���������ӣ��ϲ����գ���ժ����20��ȫ�������꣬С����������������˸��ټ�¼��������¼������ͼ����������y��kg��������ʱ��x���죩�ĺ�����ϵ��ͼ1��ӣ�Ҽ۸�z��Ԫ/kg��������ʱ��x���죩�ĺ�����ϵʽ��ͼ2��

��1����С����ӣ�ҵ���������y������ʱ��x�ĺ�������ʽ��
��2����5��x��20ʱ��ӣ�ҵļ۸�z������ʱ��x�ĺ�������ʽ��
��3������һ������۽��ﵽ������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���DAB�Ľ�ƽ�������ABC�����ƽ�����ཻ�ڵ�P���ҡ�D+��C=200�������P=( )

A. 10 �� B .20 �� C .30�� D.40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��
��0���ĶԳ�����x�ύ�ڵ�B����ֱ��l��![]() ���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
���ڵ�C����A�Ǹö��κ���ͼ����ֱ��l�ڵڶ����Ľ��㣬��D�������ߵĶ��㣬��֪AC��CO��1��2����DOB��45�㣬��ACD�����Ϊ2��
(1) �������ߵĺ�����ϵʽ��
(2) ����PΪ�����߶Գ����ϵ�һ���㣬����POC��45�������P����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=-x+1��ֱ��y=x-2�ཻ�ڵ�P���ֱ���y�ύ��A��B���㣮
��1�����P�����ꣻ
��2�����ABP�������
��3��M��N�ֱ���ֱ��y=-x+1��y=x-2�ϵ��������㣬��MN��y�ᣬ��MN=5��ֱ��д��M��N��������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB�ֱ����������ύ�ڵ�A��6��0����B��0��12������C������Ϊ��3��0��
��1����ֱ��AB�Ľ���ʽ��
��2�����߶�AB����һ����P��
������P�ֱ���x��y��Ĵ��ߣ�����ֱ�Ϊ��E��F��������OEPF�����Ϊ16�����P�����꣮
������CP���Ƿ���ڵ�P��ʹ��ACP����AOB���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com