
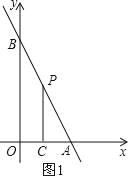
【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣2x+12;(2)①点P(2,8)或(4,4);②存在,点P的坐标为(3,6)或点P(![]() ,
,![]() )
)
【解析】
试题(1)由于A(6,0),B(0,12),利用待定系数法即可求出直线AB的解析式;
(2)①可以设动点P(x,﹣2x+12),由此得到PE=x,PF=﹣2x+12,再利用矩形OEPF的面积为16即可求出点P的坐标;
②存在,分两种情况:第一种由CP∥OB得△ACP∽△AOB,由此即可求出P的坐标;第二种CP⊥AB,根据已知条件可以证明APC∽△AOB,然后利用相似三角形的对应边成比例即可求出PA,再过点P作PH⊥x轴,垂足为H,由此得到PH∥OB,进一步得到△APH∽△ABO,然后利用相似三角形的对应边成比例就可以求出点P的坐标.
解:(1)设直线AB的解析式为y=kx+b,如图1:
依题意,![]() ,
,
∴![]() ,
,
∴y=﹣2x+12;
(2)①设动点P (x,﹣2x+12),则PE=x,PF=﹣2x+12,
∴SOEPF=PEPF=x(﹣2x+12)=16,
∴x1=2,x2=4;
经检验x1=2,x2=4都符合题意,
∴点P(2,8)或(4,4);
②存在,分两种情况
∵A(6,0),B(0,12),
∴OA=6,OB=12,AB=6![]()
第一种:CP∥OB,
∴△ACP∽△AOB,
而点C的坐标为(3,0),
∴点P(3,6);
第二种CP⊥AB,
∵∠APC=∠AOB=90°,∠PAC=∠BAO,
∴△APC∽△AOB,
∴![]() ,
,
∴![]() ,
,
∴AP=![]() ,
,
如图2,过点P作PH⊥x轴,垂足为H,
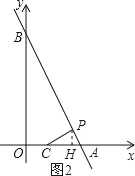
∴PH∥OB,
∴△APH∽△ABO,
∴![]() ,
,
∴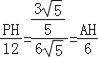 ,
,
∴PH=![]() ,AH=
,AH=![]() ,
,
∴OH=OA﹣AH=6﹣![]() =
=![]() ,
,
∴点P(![]() ,
,![]() ).
).
∴点P的坐标为(3,6)或点P(![]() ,
,![]() ).
).


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() :
:![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)如图1,点E是线段OB的中点,连结AE,点F是射线OG上一点, 当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
(3)如图2,若![]() ,过
,过![]() 点作
点作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,此时在
,此时在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
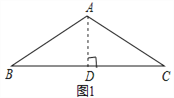
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α,
(1)如图1所示,当α=60°时,求证:△DCE是等边三角形;
(2)如图2所示,当α=45°时,求证:![]() =
=![]() ;
;
(3)如图3所示,当α为任意锐角时,请直接写出线段CE与DE的数量关系:![]() =_____.
=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
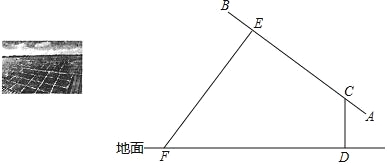
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com