
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α,
(1)如图1所示,当α=60°时,求证:△DCE是等边三角形;
(2)如图2所示,当α=45°时,求证:![]() =
=![]() ;
;
(3)如图3所示,当α为任意锐角时,请直接写出线段CE与DE的数量关系:![]() =_____.
=_____.



【答案】1
【解析】试题(1)证明△CFD≌△DAE即可解决问题.
(2)如图2中,作FG⊥AC于G.只要证明△CFD∽△DAE,推出![]() =
=![]() ,再证明CF=
,再证明CF=![]() AD即可.
AD即可.
(3)证明EC=ED即可解决问题.
试题解析:(1)证明:如图1中,∵∠ABC=∠ACB=60°,∴△ABC是等边三角形,∴BC=BA.∵DF∥AC,∴∠BFD=∠BCA=60°,∠BDF=∠BAC=60°,∴△BDF是等边三角形,∴BF=BD,∴CF=AD,∠CFD=120°.∵AE∥BC,∴∠B+∠DAE=180°,∴∠DAE=∠CFD=120°.∵∠CDA=∠B+∠BCD=∠CDE+∠ADE.∵∠CDE=∠B=60°,∴∠FCD=∠ADE,∴△CFD≌△DAE,∴DC=DE.∵∠CDE=60°,∴△CDE是等边三角形.

(2)证明:如图2中,作FG⊥AC于G.∵∠B=∠ACB=45°,∴∠BAC=90°,∴△ABC是等腰直角三角形.∵DF∥AC,∴∠BDF=∠BAC=90°,∴∠BFD=45°,∠DFC=135°.∵AE∥BC,∴∠BAE+∠B=180°,∴∠DFC=∠DAE=135°.∵∠CDA=∠B+∠BCD=∠CDE+∠ADE.∵∠CDE=∠B=45°,∴∠FCD=∠ADE,∴△CFD∽△DAE,∴![]() =
=![]() .∵四边形ADFG是矩形,FC=
.∵四边形ADFG是矩形,FC=![]() FG,∴FG=AD,CF=
FG,∴FG=AD,CF=![]() AD,∴
AD,∴![]() =
=![]() .
.

(3)解:如图3中,设AC与DE交于点O.

∵AE∥BC,∴∠EAO=∠ACB.∵∠CDE=∠ACB,∴∠CDO=∠OAE.∵∠COD=∠EOA,∴△COD∽△EOA,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .∵∠COE=∠DOA,∴△COE∽△DOA,∴∠CEO=∠DAO.∵∠CED+∠CDE+∠DCE=180°,∠BAC+∠B+∠ACB=180°.∵∠CDE=∠B=∠ACB,∴∠EDC=∠ECD,∴EC=ED,∴
.∵∠COE=∠DOA,∴△COE∽△DOA,∴∠CEO=∠DAO.∵∠CED+∠CDE+∠DCE=180°,∠BAC+∠B+∠ACB=180°.∵∠CDE=∠B=∠ACB,∴∠EDC=∠ECD,∴EC=ED,∴![]() =1.
=1.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+1和直线y=x-2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=-x+1和y=x-2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自驾游是当今社会一种重要的旅游方式,五一放假期间小明一家人自驾去灵山游玩,下图描述了小明爸爸驾驶的汽车在一段时间内路程s(千米)与时间t(小时)的函数关系,下列说法中正确的是( )

A. 汽车在0~1小时的速度是60千米/时; B. 汽车在2~3小时的速度比0~0.5小时的速度快;
C. 汽车从0.5小时到1.5小时的速度是80千米/时; D. 汽车行驶的平均速度为60千米/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:在函数y=|x|﹣2中,自变量x可以是任意实数;
Ⅰ如表是y与x的几组对应值.
y | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
x | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m= ;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n= ;
Ⅱ如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:
①该函数的最小值为 ;
②该函数的另一条性质是 .
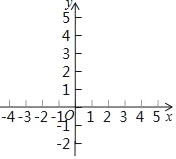
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).
(1)求直线AB的函数表达式;
(2)直线AB上有一点P,使得△PBC的面积等于9,求点P的坐标;
(3)设点D与A、B、C 点构成平行四边形,直接写出所有符合条件的点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (![]() )2016 B. (
)2016 B. (![]() )2017 C. (
)2017 C. (![]() )2016 D. (
)2016 D. (![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)点D是抛物线上的一动点,是否存在点D,使得tan∠DCB=tan∠ACO.若存在,请求出点D的坐标,若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com