
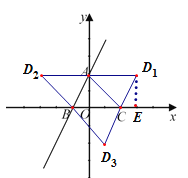
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).
(1)求直线AB的函数表达式;
(2)直线AB上有一点P,使得△PBC的面积等于9,求点P的坐标;
(3)设点D与A、B、C 点构成平行四边形,直接写出所有符合条件的点D的坐标.

【答案】(1)y=2x+2;(2)(2,6)或(-4,-6);(3)(3,2)、(-3,2)、(1,-2)
【解析】
(1)根据待定系数法,可得函数解析式;
(2)设点P的坐标为(x,2x+2),根据三角形的面积公式列方程求解即可;
(3)分三种情况求解即可:①当AB、BC为邻边时,②当AB为对角线时,③当BC为对角线时.
解:(1)设直线AB的函数解析式为y=kx+b,
∵直线AB经过点A(0,2)、B(-1,0),得
![]() ,
,
解得![]() .
.
∴直线AB的函数解析式为y=2x+2;
(2)由题意,设点P的坐标为(x,2x+2),
S△POA=![]() ×BC×|py|=
×BC×|py|=![]() ×3×|2x+2|=9.
×3×|2x+2|=9.
解得x=2或x=-4.
故点P的坐标是(2,6)或(-4,-6);
(3)①当AB、BC为邻边时,作D1E⊥BC于E,
∵四边形ABCD1是平行四边形,
∴AD1=BC=3,AB=CD1,∠ABC=∠D1CE,
又∵∠AOB=∠D1EC,
∴△AOB≌△D1EC,
∴CE=BO=1,
∴D1(3,2);
同理可求:
②当AB为对角线时,D2(-3,2);
③当BC为对角线时,D3(1,-2);
综上所述:点D与A、B、C点构成平行四边形,点D的坐标为(3,2)、(-3,2)、(1,-2).


科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
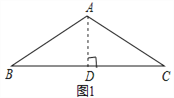
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
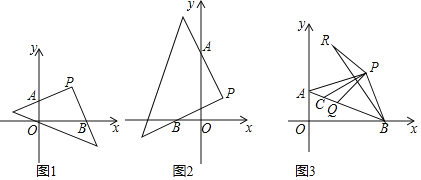
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α,
(1)如图1所示,当α=60°时,求证:△DCE是等边三角形;
(2)如图2所示,当α=45°时,求证:![]() =
=![]() ;
;
(3)如图3所示,当α为任意锐角时,请直接写出线段CE与DE的数量关系:![]() =_____.
=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
(1)求证:① △AEF≌△DEB;② 四边形ADCF是平行四边形;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明口袋中装有![]() 个红球、
个红球、![]() 个白球、
个白球、![]() 个黄球,每个球除颜色外其他均相同.从这个口袋中同时摸出两个球,发生概率最小的事件是摸到( )
个黄球,每个球除颜色外其他均相同.从这个口袋中同时摸出两个球,发生概率最小的事件是摸到( )
A. 都是红球 B. 一个红球,一个白球
C. 都是白球 D. 一个白球,一个黄球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:点P(a,b),P点坐标满足![]() +|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
+|3a﹣2b﹣4|=0将45°角的三角板,直角顶点放在P处,两边与坐标轴交于A、B两点,如图1,求a、b的值.
(2)将三角板绕P点,顺时针旋转,两边与x轴交于B点,与y轴交于A点,求|OA﹣OB|的值.
(3)如图3,若Q是线段AB上一动点,C为AQ中点,PR⊥PQ且PR=PQ,连BR,请同学们判断线段BR与PC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
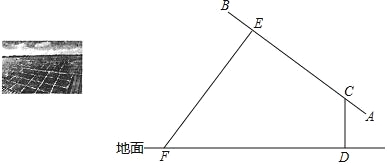
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中线段AB、CD、EF表示支撑角钢,太阳能电池板紧贴在支撑角钢AB上且长度均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD、EF与地面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学的家与学校的距离均为![]() .甲同学先步行
.甲同学先步行![]() ,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的
,然后乘公交车去学校;乙同学骑自行车去学校.已知乙同学骑自行车的速度是甲同学步行速度的一倍,公交车的速度是乙同学骑自行车速度的![]() 倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到
倍.甲、乙两名同学同时从家出发去学校,结果甲同学比乙同学早到![]() .
.
(1)解:设乙同学骑自行车的速度为![]() .完成表格:
.完成表格:
乙同学 | 甲同学 | ||
骑自行车 | 步行 | 乘公交车 | |
路程 |
|
| |
时间 |
| ||
(2)求乙同学骑自行车的速度.
(3)当甲同学到达学校时,乙同学离学校还有多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com