
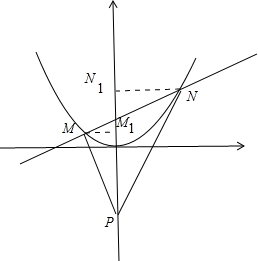
 ��ͼ��������y=ax2+bx+c����ֱ��x=-1�Գƣ��������ύ��A��B��C���㣬��AB=4����D������Ϊ��-2��-
��ͼ��������y=ax2+bx+c����ֱ��x=-1�Գƣ��������ύ��A��B��C���㣬��AB=4����D������Ϊ��-2��-| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
|
| 2 |
| k |
|
| 7 |
| 2k |
| 3 |
| 2 |
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
| 11 |
| 5 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MM1 |
| NN1 |
| PM1 |
| PN1 |
| -xm |
| xn |
| -t+ym |
| -t+yn |
| xm |
| xn |
| t-ym |
| t-yn |
| xm |
| xn |
| t-kxm-2 |
| t-kxn-2 |


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
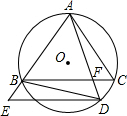 ��ͼ����ABC�ڽ��ڡ�O����D�ڻ�BC�ϣ�����D��DE��BC����ֱ��AB�ڵ�E������AD��BC�ڵ�F������BD������ADB=��E��
��ͼ����ABC�ڽ��ڡ�O����D�ڻ�BC�ϣ�����D��DE��BC����ֱ��AB�ڵ�E������AD��BC�ڵ�F������BD������ADB=��E��| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
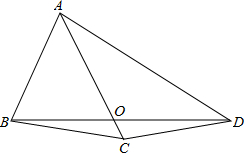 ��ͼ�����ı���ABCD�У��߶�AC��BD�ཻ��O��AB=BC=CD����ABC=70�㣬��BCD=170�㣬���BAD�Ķ�����
��ͼ�����ı���ABCD�У��߶�AC��BD�ཻ��O��AB=BC=CD����ABC=70�㣬��BCD=170�㣬���BAD�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 4 |
| 3 |
| 4t |
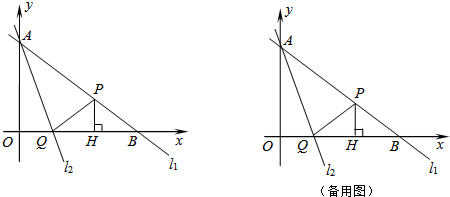
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
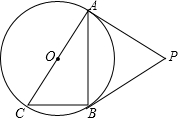 ��ͼ����O��Rt��ABC�����Բ����ABC=90�㣬��P��Բ��һ�㣬PA�С�O�ڵ�A����PA=PB��
��ͼ����O��Rt��ABC�����Բ����ABC=90�㣬��P��Բ��һ�㣬PA�С�O�ڵ�A����PA=PB��| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
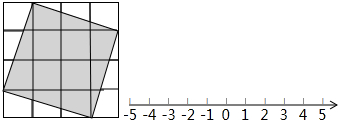
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com