
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②s=![]() (0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).
(0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).
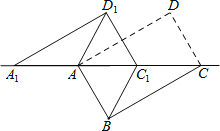
【答案】①②④
【解析】
试题分析:①根据矩形的性质,得∠DAC=∠ACB,再由平移的性质,可得出∠A1=∠ACB,A1D1=CB,从而证出结论;
②易得△AC1F∽△ACD,根据面积比等于相似比平方可得出s与x的函数关系式
③根据菱形的性质,四条边都相等,可推得当C1在AC中点时四边形ABC1D1是菱形.
④当x=2时,点C1与点A重合,可求得BD=DD1=BD1=2,从而可判断△BDD1为等边三角形.
解:①∵四边形ABCD为矩形,
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,
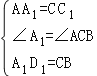 ,
,
∴△A1AD1≌△CC1B(SAS),
故①正确;
②易得△AC1F∽△ACD,
∴![]()
解得:S△AC1F=![]() (x﹣2)2 (0<x<2);故②正确;
(x﹣2)2 (0<x<2);故②正确;
③∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=D1C1,
又AB∥BC1,
∴四边形ABC1D1是菱形,
故③错误;
④如图所示:
则可得BD=DD1=BD1=2,
∴△BDD1为等边三角形,故④正确.
综上可得正确的是①②④.
故答案为:①②④


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.

已知: .
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列问题用到推理的是( )
A. 根据x=1,y=1,得x=y
B. 观察得到的四边形有四个内角
C. 老师告诉了我们关于金字塔的许多奥秘
D. 由公理知道过两点有且只有一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A. (7m+4n)元 B. 28mn元 C. (4m+7n)元 D. 11mn元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据深圳统计局公布数据,2015年深圳公共财政收入达7240亿元,同比增长30.2%,数据“7240亿”用科学记数法表示为( )
A.0.724×1013 B.7.24×1012 C.7.24×1011 D.72.4×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
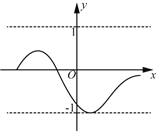
(1)分别判断函数 y=![]() (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数 y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足![]() ≤t≤1?
≤t≤1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
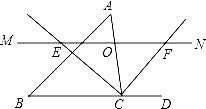
(1)若CE=12,CF=5,求OC的长;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com