
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1B1C1 , AB与A1C1相交于点D,A1C1、BC1与AC分别交于点E、F. 
(1)求证:△BCF≌△BA1D;
(2)当∠C=40°时,请你证明四边形A1BCE是菱形.
【答案】
(1)解:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
∵将等腰△ABC绕顶点B逆时针方向旋转40度到△A1BC1的位置,
∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,
在△BCF与△BA1D中,
 ,
,
∴△BCF≌△BA1D(ASA);
(2)解:∵∠C=40°,△ABC是等腰三角形,
∴∠A=∠C1=∠C=40°,
∴∠C1=∠CBF=40°,∠A=∠A1BD=40°,
∴A1E∥BC,A1B∥CE,
∴四边形A1BCE是平行四边形,
∵A1B=BC,
∴四边形A1BCE是菱形.

【解析】(1)根据旋转的性质,得出A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1 , 再根据ASA即可判定△BCF≌△BA1D;(2)根据∠C=40°,△ABC是等腰三角形,即可得出∠A=∠C1=∠C=40°,进而得到∠C1=∠CBF,∠A=∠A1BD,由此可判定A1E∥BC,A1B∥CE,进而得到四边形A1BCE是平行四边形,最后根据A1B=BC,即可判定四边形A1BCE是菱形.
【考点精析】本题主要考查了等腰三角形的性质和菱形的判定方法的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】为了进一步了解义务教育阶段学生的体质健康状况,教育部对我市某中学九年级的部分学生进行了体质检测.体质检测的结果分为四个等级:优秀、良好、合格、不合格:根据调查结果绘制了下列两幅不完整的统计图,请你根据统计图提供的信息回答以下问题: 
(1)在扇形统计图中,“合格”的百分比为多少?
(2)将条形统计图补充完整:
(3)若该校九年级有400名学生,估计该校九年级体质为“不合格”,等级的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 
A.36
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图: ①分别以B、C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
A.50°
B.45°
C.30°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],那么第35秒时质点所在位置的坐标是( ) 
A.(4,0)
B.(0,5)
C.(5,0)
D.(5,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠A=90°,AB=6,AD=4,DC=3,动点P从点A出发,沿A→D→C→B方向移动,动点Q从点A出发,在AB边上移动.设点P移动的路程为x,点Q移动的路程为y,线段PQ平分梯形ABCD的周长.
(1)求y与x的函数关系式,并求出x,y的取值范围;
(2)当PQ∥AC时,求x,y的值;
(3)当P不在BC边上时,线段PQ能否平分梯形ABCD的面积?若能,求出此时x的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.![]()
B.![]()
C.π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( ) 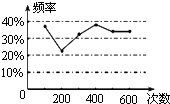
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com