

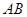 中点
中点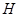 ,联结
,联结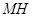 ,
,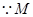 为
为 的中点,
的中点,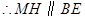 ,
,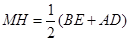 .
. 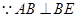 ,
,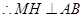 .
.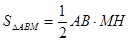 ,得
,得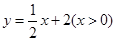 ;
; 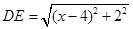 .
.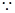 以线段AB为直径的圆与以线段DE为直径的圆外切,
以线段AB为直径的圆与以线段DE为直径的圆外切, ,
, 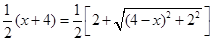 .
. 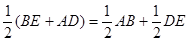
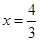 ,即线段
,即线段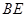 的长为
的长为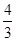 ;
;  为顶点的三角形与
为顶点的三角形与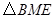 相似,
相似,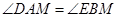 .
.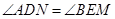 ;②
;②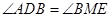 .
. 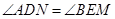 时,
时, ,
,
 .
.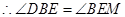 .
. ,易得
,易得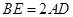 .得
.得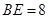 ;
; 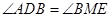
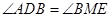 时,
时, ,
,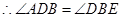 .
. .又
.又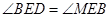 ,
,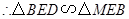 .
.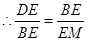 ,即
,即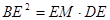 ,
, 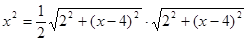 .
.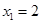 ,
, (舍去).即线段BE的长为2.
(舍去).即线段BE的长为2. 

科目:初中数学 来源:不详 题型:解答题
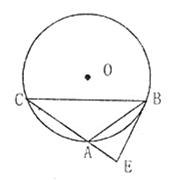
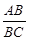 =
=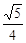 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=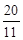 ,求AC的值。
,求AC的值。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

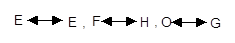 (3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
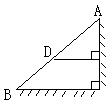
| A.3.85米 | B.4.00米 | C.4.40米 | D.4.50米 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

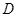 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米,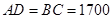 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道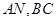 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于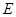 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.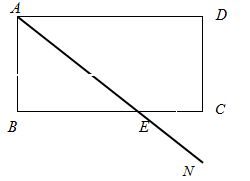
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
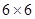 的正方形网格,⊿ABC是格点三角形(顶点在小正方形顶点上).
的正方形网格,⊿ABC是格点三角形(顶点在小正方形顶点上).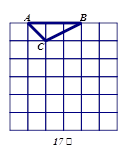
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
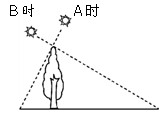
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com