
 ;
;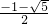 或x≥
或x≥ ;
;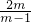 >0,x1•x2=-
>0,x1•x2=- >0,
>0, ≤x<1时,方程有两个正实数根,
≤x<1时,方程有两个正实数根, ≤x≤1.
≤x≤1. ;当m-1≠0,即m≠1,设方程的两实数根为x1,x2,根据根的判别式得到△=4m2-4(m-1)×(-1)≥0,可解得x≤
;当m-1≠0,即m≠1,设方程的两实数根为x1,x2,根据根的判别式得到△=4m2-4(m-1)×(-1)≥0,可解得x≤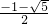 或x≥
或x≥ ;
;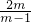 >0,x1•x2=-
>0,x1•x2=- >0,由于m-1<0,则2m>0,于是0<m<1,然后纵综合两种情况即可得到m的范围.
>0,由于m-1<0,则2m>0,于是0<m<1,然后纵综合两种情况即可得到m的范围.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com