
分析 (1)首先化简x(x+2y)-(x-1)2+2x,然后把x=$\frac{1}{25}$,y=-25代入化简后的算式,求出算式的是多少即可.
(2)首先化简4(x2+y)-(2x2-y)2,然后把x=2,y=-5代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)x(x+2y)-(x-1)2+2x
=x2+2xy-x2+2x-1+2x
=4x+2xy-1
当x=$\frac{1}{25}$,y=-25时,
原式=4×$\frac{1}{25}$+2×$\frac{1}{25}$×(-25)-1
=$\frac{4}{25}$-2-1
=-2$\frac{21}{25}$
(2)4(x2+y)-(2x2-y)2
=4x2+4y-4x4-y2+4x2y
当x=2,y=-5时,
原式=4×4+4×(-5)-4×16-25+4×4×(-5)
=16-20-64-25-80
=-173
点评 此题主要考查了整式的混合运算-化简求值问题,要熟练掌握,解答此题的关键是要明确:先按运算顺序把整式化简,再把对应字母的值代入求整式的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
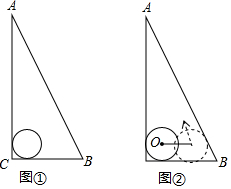 如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com