
如图,已知直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点D,抛物线
轴交于点D,抛物线![]() 与直线交于A、E两点,与
与直线交于A、E两点,与![]() 轴交于B、C两点,且B点坐标为 (1,0)。
轴交于B、C两点,且B点坐标为 (1,0)。![]()
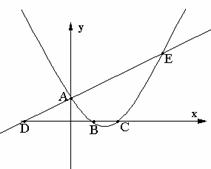
⑴求该抛物线的解析式;
⑵动点P在轴上移动,当△PAE是直角三角形时,求点P的坐标P。
⑶在抛物线的对称轴上找一点M,使![]() 的值最大,求出点M的坐标。
的值最大,求出点M的坐标。
(1)将A(0,1)、B(1,0)坐标代入![]() 得
得 解得
解得
∴抛物线的解折式为![]()
(2)设点E的横坐标为m,则它的纵坐标为 ![]()
即 E点的坐标(![]() ,
,![]() )又∵点E在直线
)又∵点E在直线![]() 上
上
∴![]() 解得
解得![]() (舍去),
(舍去),![]()
∴E的坐标为(4,3)

(Ⅰ)当A为直角顶点时
过A作AP1⊥DE交x轴于P1点,设P1(a,0) 易知D点坐标为(-2,0) 由Rt△AOD∽Rt△POA得
![]() 即
即![]() ,∴a=
,∴a=![]() ∴P1(
∴P1(![]() ,0)
,0)
(Ⅱ)同理,当E为直角顶点时,P2点坐标为(![]() ,0)
,0)
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(![]() 、
、![]() )由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
)由∠OPA+∠FPE=90°,得∠OPA=∠FEP Rt△AOP∽Rt△PFE
由![]() 得
得![]() 解得
解得![]() ,
,![]()
∴此时的点P3的坐标为(1,0)或(3,0)
综上所述,满足条件的点P的坐标为(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0)
,0)
(Ⅲ)抛物线的对称轴为![]()
∵B、C关于x=![]() 对称 ∴MC=MB
对称 ∴MC=MB
要使![]() 最大,即是使
最大,即是使![]() 最大
最大
由三角形两边之差小于第三边得,当A、B、M在同一直线上时![]() 的值最大.
的值最大.
易知直线AB的解折式为![]() ∴由
∴由 得
得 ∴M(
∴M(![]() ,-
,-![]() )
)


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
 轴交于A(1,0),B(
轴交于A(1,0),B(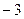 ,0)两点,与
,0)两点,与 轴交于点
轴交于点 轴交于点Q,求点D的坐标;
轴交于点Q,求点D的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
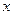 轴交于点
轴交于点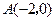 ,
,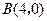 ,与
,与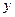 轴交于点
轴交于点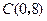 .
.
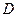 的坐标;
的坐标;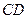 交
交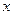 轴于点
轴于点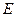 .在线段
.在线段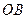 的垂直平分线上是否存在点
的垂直平分线上是否存在点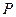 ,使得点
,使得点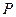 到直线
到直线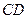 的距离等于点
的距离等于点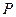 到原点
到原点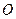 的距离?如果存在,求出点
的距离?如果存在,求出点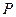 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;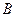 作
作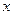 轴的垂线,交直线
轴的垂线,交直线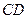 于点
于点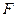 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段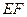 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州市九年级第一学期期末考试数学卷 题型:解答题
.(10分)如图,已知抛物线与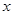 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点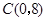 .
.
【小题1】(1)求抛物线的解析式及其顶点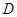 的坐标;
的坐标;
【小题2】(2)设直线 交
交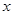 轴于点
轴于点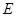 .在线段
.在线段 的垂直平分线上是否存在点
的垂直平分线上是否存在点 ,使得点
,使得点 到直线
到直线 的距离等于点
的距离等于点 到原点
到原点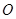 的距离?如果存在,求出点
的距离?如果存在,求出点 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
【小题3】(3)过点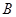 作
作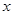 轴的垂线,交直线
轴的垂线,交直线 于点
于点 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知直线![]() 与
与![]() 轴交于A点,与
轴交于A点,与![]() 轴交于B点,点M的坐标为(4,0),点P(
轴交于B点,点M的坐标为(4,0),点P(![]() ,
,![]() )是第一象限内直线AB上的动点,连接OP、MP. 设△OPM的面积为s.
)是第一象限内直线AB上的动点,连接OP、MP. 设△OPM的面积为s.
(1)求s关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的取值范围;
的取值范围;
(2)当P点在什么位置时,图中存在与△OPM全等的三角形?画出所有符合条件的示意图,并说明全等的理由(不能添加其他字母和其他辅助线);
(3)在(2)的条件下,求P点坐标.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com