
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжагаRtЁїABCЃЌЁЯAЃН90ЁуЃЌABЃНACЃЌAЃЈЃ2ЃЌ0ЃЉЁЂBЃЈ0ЃЌ dЃЉЁЂCЃЈЃ3ЃЌ2ЃЉ.
ЃЈ1ЃЉЧѓdЕФжЕЃЛ
ЃЈ2ЃЉНЋЁїABCби![]() жсЕФе§ЗНЯђЦНвЦaИіЕЅЮЛЃЌдкЕквЛЯѓЯоФкBЁЂCСНЕуЕФЖдгІЕуBЁфЁЂCЁфе§КУТфдкФГЗДБШР§КЏЪ§ЭМЯёЩЯ.ЧыЧѓГіетИіЗДБШР§КЏЪ§КЭДЫЪБжБЯпBЁфCЁфЕФНтЮіЪНЃЛ
жсЕФе§ЗНЯђЦНвЦaИіЕЅЮЛЃЌдкЕквЛЯѓЯоФкBЁЂCСНЕуЕФЖдгІЕуBЁфЁЂCЁфе§КУТфдкФГЗДБШР§КЏЪ§ЭМЯёЩЯ.ЧыЧѓГіетИіЗДБШР§КЏЪ§КЭДЫЪБжБЯпBЁфCЁфЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБЯп![]() НЛyжсгкЕуGЃЌзї
НЛyжсгкЕуGЃЌзї![]() ЁЭ
ЁЭ![]() жсгк
жсгк![]() ЃЎ
ЃЎ ![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛЕуЃЌШєЁї
ЩЯЕФвЛЕуЃЌШєЁї![]() КЭЁї
КЭЁї![]() УцЛ§ЯрЕШЃЌЧѓЕу
УцЛ§ЯрЕШЃЌЧѓЕу![]() зјБъЃЎ
зјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉ1ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
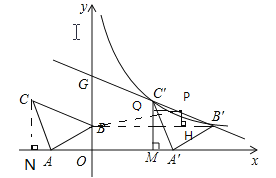
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉзїCNЁЭxжсгкЕуNЃЌжЄУїRtЁїCNAКЭRtЁїAOBЃЌОнДЫМДПЩЧѓГіAN=OB=1ЃЌНјЖјЕУНтЃЛ
ЃЈ2ЃЉЗжБ№гУКЌгаaЕФДњЪ§ЪНБэЪОГіЕуBЁфЃЌCЁфЕФзјБъЃЌВЂгУД§ЖЈЯЕЪ§ЗЈЧѓЗДБШР§КЏЪ§НтЮіЪНЃЌМДПЩЕУНтЃЛ
ЃЈ3ЃЉЩшГіЕуPЕФзјБъЃЌИљОнУцЛ§ЯрЕШЕУЕНЗНГЬЃЌОнДЫМДПЩЕУНтЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉзїCNЁЭxжсгкЕуNЃЎ
дкRtЁїCNAКЭRtЁїAOBжаЃЌЁпNC=OAЃЌAC=ABЃЌЁрRtЁїCNAЁеRtЁїAOBЃЈHLЃЉЃЌдђBO=AN=3Љ2=1ЃЌЁрd=1ЃЛ
ЃЈ2ЃЉЩшЗДБШР§КЏЪ§ЮЊ![]() ЃЌЕуCЁфКЭBЁфдкИУБШР§КЏЪ§ЭМЯѓЩЯЃЌЩшCЁфЃЈaЃЌ2ЃЉЃЌдђBЁфЃЈa+3ЃЌ1ЃЉЃЌАбЕуCЁфКЭBЁфЕФзјБъЗжБ№ДњШы
ЃЌЕуCЁфКЭBЁфдкИУБШР§КЏЪ§ЭМЯѓЩЯЃЌЩшCЁфЃЈaЃЌ2ЃЉЃЌдђBЁфЃЈa+3ЃЌ1ЃЉЃЌАбЕуCЁфКЭBЁфЕФзјБъЗжБ№ДњШы![]() ЃЌЕУk=2aЃЛk=a+3ЃЌЁр2a=a+3ЃЌa=3ЃЌдђk=6ЃЌЗДБШР§КЏЪ§НтЮіЪНЮЊ
ЃЌЕУk=2aЃЛk=a+3ЃЌЁр2a=a+3ЃЌa=3ЃЌдђk=6ЃЌЗДБШР§КЏЪ§НтЮіЪНЮЊ![]() ЃЎЕУЕуCЁфЃЈ3ЃЌ2ЃЉЃЛBЁфЃЈ6ЃЌ1ЃЉЃЛ
ЃЎЕУЕуCЁфЃЈ3ЃЌ2ЃЉЃЛBЁфЃЈ6ЃЌ1ЃЉЃЛ
ЩшжБЯпCЁфBЁфЕФНтЮіЪНЮЊy=ax+bЃЌАбCЁфЁЂBЁфСНЕузјБъДњШыЕУЃК ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК 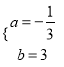 ЃЛ
ЃЛ
ЁржБЯпCЁфBЁфЕФНтЮіЪНЮЊЃКy=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНсBBЁфЃЎЁпBЃЈ0ЃЌ1ЃЉЃЌBЁфЃЈ6ЃЌ1ЃЉЃЌЁрBBЁфЁЮxжсЃЌЩшPЃЈmЃЌ ![]() ЃЉЃЌзїPQЁЭCЁфMЃЌPHЁЭBBЁфЃЌЁрSЁїPCЁЏM=
ЃЉЃЌзїPQЁЭCЁфMЃЌPHЁЭBBЁфЃЌЁрSЁїPCЁЏM=![]() ЁСPQЁСCЁфM=
ЁСPQЁСCЁфM=![]() ЁСЃЈmЉ3ЃЉЁС2=mЉ3
ЁСЃЈmЉ3ЃЉЁС2=mЉ3
SЁїPBBЁЏ=![]() ЁСPHЁСBBЁф=
ЁСPHЁСBBЁф=![]() ЁСЃЈ
ЁСЃЈ![]() ЃЉЁС6=Љm+6
ЃЉЁС6=Љm+6
ЁрmЉ3=Љm+6
Ёрm=![]()
ЁрPЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
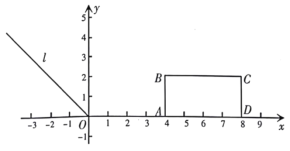
ЁОЬтФПЁПШчЭМЃЌгаAаЭЁЂBаЭЁЂCаЭШ§жжВЛЭЌЕФжНАхЃЌЦфжаAаЭЃКБпГЄЮЊaРхУзЕФе§ЗНаЮЃЛBаЭЃКГЄЮЊaРхУзЃЌПэЮЊ1РхУзЕФГЄЗНаЮЃЛCаЭЃКБпГЄЮЊ1РхУзЕФе§ЗНаЮ.
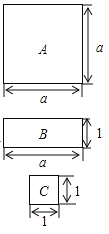
ЃЈ1ЃЉAаЭ2ПщЃЌBаЭ4ПщЃЌCаЭ4ПщЃЌДЫЪБжНАхЕФзмУцЛ§ЮЊ ЦНЗНРхУзЃЛ
ЂйДгет10ПщжНАхжаФУЕє1ПщAаЭжНАхЃЌЪЃЯТЕФжНАхдкВЛжиЕўЕФЧщПіЯТЃЌПЩвдНєУмЕФХХГівЛИіДѓе§ЗНаЮЃЌетИіДѓе§ЗНаЮЕФБпГЄЮЊ РхУзЃЛ
ЂкДгет10ПщжНАхжаФУЕє2ПщЭЌРраЭЕФжНАхЃЌЪЙЕУЪЃЯТЕФжНАхдкВЛжиЕўЕФЧщПіЯТЃЌПЩвдНєУмЕиХХГіСНИіЯрЭЌЕФДѓе§ЗНаЮЃЌЧыЮЪФУЕєЕФЪЧ2ПщФФжжРраЭЕФжНАхЃПЃЈМЦЫуЫЕУїЃЉ
ЃЈ2ЃЉAаЭ12ПщЃЌBаЭ12ПщЃЌCаЭ4ПщЃЌДгет28ПщжНАхжаФУЕє1ПщжНАхЃЌЪЙЕУЪЃЯТЕФжНАхдкВЛжиЕўЕФЧщПіЯТЃЌПЩвдНєУмЕиХХГіШ§ИіЯрЭЌаЮзДЕФДѓе§ЗНаЮЃЌдђДѓе§ЗНаЮЕФБпГЄЮЊ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП.ЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЃЌИјГіЯТСаЫФИіНсТлЃКЂй4acЉb2ЃМ0ЃЛЂк4a+cЃМ2bЃЛЂл3b+2cЃМ0ЃЛЂмmЃЈam+bЃЉ+bЃМaЃЈmЁйЉ1ЃЉЃЌЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
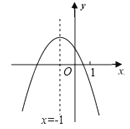
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСаЗНГЬНтгІгУЬтЃКФГЭцОпГЇЩњВњвЛжжЭцОпЃЌАДееПижЦЙЬЖЈГЩБОНЕМлДйЯњЕФддђЃЌЪЙЩњВњЕФЭцОпФмЙЛМАЪБЪлГіЃЌОнЪаГЁЕїВщЃКУПИіЭцОпАД480дЊЯњЪлЪБЃЌУПЬьПЩЯњЪл160ИіЃЛШєЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌУПЬьПЩЖрЪлГі2ИіЃЌвбжЊУПИіЭцОпЕФЙЬЖЈГЩБОЮЊ360дЊЃЌЮЪетжжЭцОпЕФЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌГЇМвУПЬьПЩЛёРћШѓзюЖрЃПзюЖрЛёРћЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРћУёЩЬГЁОгЊФГжжЦЗХЦЕФTаєЃЌЙКНјЪБЕФЕЅМлЪЧ300дЊЃЌИљОнЪаГЁЕїВщЃКдквЛЖЮЪБМфФкЃЌЯњЪлЕЅМлЪЧ400дЊЪБЃЌЯњЪлСПЪЧ60МўЃЌЯњЪлЕЅМлУПеЧ10дЊЃЌЯњЪлСПОЭМѕЩй1МўЃЎЩшетжжTаєЕФЯњЪлЕЅМлЮЊxдЊЃЈxЃО400ЃЉЪБЃЌЯњЪлСПЮЊyМўЁЂЯњЪлРћШѓЮЊWдЊЃЎ
ЃЈ1ЃЉЧыЗжБ№гУКЌxЕФДњЪ§ЪНБэЪОyКЭWЃЈАбНсЙћЬюШыЯТБэЃЉЃК
ЯњЪлЕЅМлЃЈдЊЃЉ | x |
ЯњЪлСПyЃЈМўЃЉ | |
ЯњЪлРћШѓWЃЈдЊЃЉ |
ЃЈ2ЃЉИУЩЬГЁМЦЛЎЪЕЯжЯњЪлРћШѓ10000дЊЃЌВЂОЁПЩФмдіМгЯњЪлСПЃЌФЧУДxЕФжЕгІЕБЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊГЄЗНаЮ![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШчЭМЃЌгавЛЖЏЕу![]() дкЕкЖўЯѓЯоЕФНЧЦНЗжЯп
дкЕкЖўЯѓЯоЕФНЧЦНЗжЯп![]() ЩЯЃЌШє
ЩЯЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєАбГЄЗНаЮ![]() ЯђЩЯЦНвЦЃЌЕУЕНГЄЗНаЮ
ЯђЩЯЦНвЦЃЌЕУЕНГЄЗНаЮ![]() .
.
ЂйдкдЫЖЏЙ§ГЬжаЃЌЧѓ![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() ЕФУцЛ§жЎМфЕФЪ§СПЙиЯЕЃЛ
ЕФУцЛ§жЎМфЕФЪ§СПЙиЯЕЃЛ
ЂкШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() ЕФУцЛ§жЎБШ.
ЕФУцЛ§жЎБШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЪщЯуГЄЩГ2019ЪРНчЖСЪщШеЁБЯЕСажїЬтЛюЖЏМЄЗЂСЫбЇЩњЕФдФЖСаЫШЄЃЌЮваЃЮЊТњзубЇЩњЕФдФЖСашЧѓЃЌгћЙКНјвЛХњбЇЩњЯВЛЖЕФЭМЪщЃЌбЇаЃзщжЏбЇЩњЛсГЩдБЫцЛњГщШЁВПЗжбЇЩњНјааЮЪОэЕїВщЃЌБЛЕїВщбЇЩњаыДгЁАЮФЪЗРрЁЂЖХПЦРрЁЂаЁЫЕРрЁЂЩњЛюРрЁБжабЁдёздМКЯВЛЖЕФвЛРрЃЌИљОнЕїВщНсЙћЛцжЦСЫЭГМЦЭМЃЈЮДЭъГЩЃЉЃЌЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
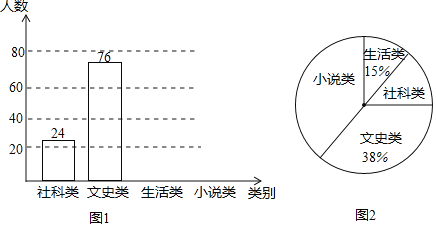
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫЁЁ ЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЭМ2жаЁАаЁЫЕРрЁБЫљдкЩШаЮЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЛ
ЃЈ4ЃЉШєИУаЃЙВгабЇЩњ3000ШЫЃЌЙРМЦИУаЃЯВЛЖЁАЮФЪЗРрЁБЪщМЎЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЗРКщДѓЕЬЕФКсНиУцШчЭМЫљЪОЃЌвбжЊAEЁЮBCЃЌБГЫЎЦТABЕФЦТЖШ![]() ЃЌЧвAB=26УзЃЎЩэИп1.8УзЕФаЁУїЪњжБеОСЂгкAЕуЃЌблОІдкMЕуДІВтЕУЪњСЂЕФИпбЙЕчЯпИЫЖЅЖЫDЕуЕФбіНЧЮЊ24ЁуЃЌвбжЊЕиУцCBПэ30УзЃЌдђИпбЙЕчЯпИЫCDЕФИпЖШдМЮЊЃЈЁЁ ЁЁЃЉЃЈНсЙћОЋШЗЕНећЪ§ЃЌВЮПМЪ§ОнЃКsin24ЁуЁж0.40ЃЌcos24ЁуЁж0.91ЃЌtan24ЁуЁж0.45ЃЉ
ЃЌЧвAB=26УзЃЎЩэИп1.8УзЕФаЁУїЪњжБеОСЂгкAЕуЃЌблОІдкMЕуДІВтЕУЪњСЂЕФИпбЙЕчЯпИЫЖЅЖЫDЕуЕФбіНЧЮЊ24ЁуЃЌвбжЊЕиУцCBПэ30УзЃЌдђИпбЙЕчЯпИЫCDЕФИпЖШдМЮЊЃЈЁЁ ЁЁЃЉЃЈНсЙћОЋШЗЕНећЪ§ЃЌВЮПМЪ§ОнЃКsin24ЁуЁж0.40ЃЌcos24ЁуЁж0.91ЃЌtan24ЁуЁж0.45ЃЉ

A. 33Уз B. 34Уз C. 35Уз D. 36Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЃЈ2aЃЋ1)2Ѓ(2aЃЋ1)(Ѓ1ЃЋ2a) ЃЈ2ЃЉ2006ЁС2008Ѓ20072
ЃЈ3ЃЉЃЈx-yЃЉ3ЁЄЃЈx-yЃЉ2ЁЄЃЈy-xЃЉ ЃЈ4ЃЉЃЈ3mn+1ЃЉЃЈ3mn-1ЃЉ-8m2n2
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com