
【题目】(1)(2a+1)2-(2a+1)(-1+2a) (2)2006×2008-20072
(3)(x-y)3·(x-y)2·(y-x) (4)(3mn+1)(3mn-1)-8m2n2
【答案】(1)4a+2;(2)-1;(3)-(x-y)6;(4)m2n2-1.
【解析】
(1)先根据完全平方公式、平方差公式把括号展开,再合并同类项即可求解;(2)把2006×2008化为(2007-1)(2007+1),再利用平方差公式展开后合并即可;(3)先把底数统一,再按照同底数幂的乘法即可求出结果;(4)先根据平方差公式把括号展开,合并同类项即可.
(1)(2a+1)2-(2a+1)(-1+2a)
= ![]()
=![]()
=4a+2;
(2)2006×2008-20072
=(2007-1)(2007+1)-20072
=20072 -1-20072
=-1;
(3)(x-y)3·(x-y)2·(y-x)
= -(x-y)3·(x-y)2·(x-y)
=-(x-y)6;
(4)(3mn+1)(3mn-1)-8m2n2
=![]() -8m2n2
-8m2n2
=m2n2-1.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0, d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿![]() 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
(3)在(2)的条件下,直线![]() 交y轴于点G,作
交y轴于点G,作![]() ⊥
⊥![]() 轴于
轴于![]() .
. ![]() 是线段
是线段![]() 上的一点,若△
上的一点,若△![]() 和△
和△![]() 面积相等,求点
面积相等,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正方形内两个相邻正方形的面积分别为 4 和 2,它们都有两个顶点在大正方形的边 上且组成的图形为轴对称图形,则图中阴影部分的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
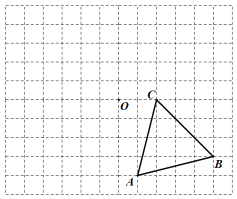
【题目】已知△ABC的顶点A、B、C在边长为1的网格格点上.
(1)画△ABC绕点O逆时针旋转90°得到的△A1B1C1;
(2)画△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)平行四边形A1B1A2B2的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
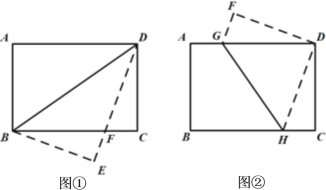
【题目】在矩形纸片ABCD中,AB=6,BC=8,
(1)将矩形纸片沿BD折叠,点A落在点E处(如图①),设DE与BC相交于点F,试说明△DBF是等腰三角形,并求出其周长.
(2)将矩形纸片折叠,使点B与点D重合(如图②),求折痕GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
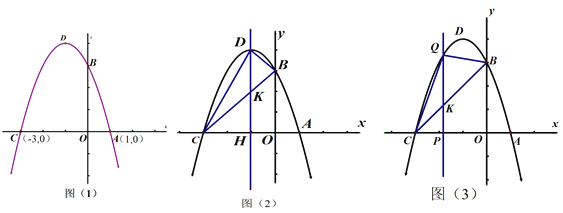
【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列短文:
如图,G是四边形ABCD对角线AC上一点,过G作GE∥CD交AD于E,GF∥CB交AB于F,若EG=FG,则有BC=CD成立,同时可知四边形ABCD与四边形AFGE相似.

解答问题:
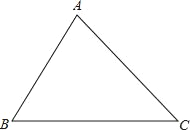
(1)有一块三角形空地(如图△ABC),BC邻近公路,现需在此空地上修建一个正方形广场,其余地为草坪,要使广场一边靠公路,且其面积最大,如何设计,请你在下面图中画出此广场正方形.(尺规作图,不写作法)
(2)锐角△ABC是一块三角形余料,边AB=130mm,BC=150mm,AC=140mm,要把它加工成正方形零件,使正方形的一边在三角形的一边上,其余两个顶点分别在另外两条边上,且剪去正方形零件后剩下的边角料较少,这个正方形零件的边长是多少?你能得出什么结论,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗洪指挥部的一位驾驶员接到一个防洪的紧急任务,要在限定的时内把一批抗洪物质从物质局运到水库,这辆车如果按每小时30千米的速度行驶在限定的时间内赶到水库,还差3千米,他决定以每小时40千米的速度前进,结果比限定时间早到18分钟,问限定时间是几小时?物质局仓库离水库有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com