
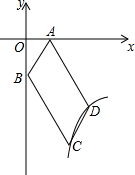
 如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).
如图,四边形ABCD是?,AD=2CD,A(1,0),B(0,-2),双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,设D(a、b).分析 (1)根据平行四边形的对边相等且平行的性质来求点C的坐标;
(2)把点D、C的坐标代入函数关系式来求k的值.
解答 解:(1)∵四边形ABCD是平行四边形,A(1,0),B(0,-2),D(a、b),
∴C(a-1,b-2);
(2)由A(1,0),B(0,-2),D(a、b),C(a-1,b-2),AD=2CD,得
$\sqrt{(a-1)^{2}+{b}^{2}}$=2$\sqrt{{1}^{2}+{2}^{2}}$,
整理,得
(a-1)2+b2=20,①
又∵双曲线y=$\frac{k}{x}$(x>0)经过C、D两点,
∴ab=(a-1)•(b-2),②
①②联立,得
a=5,b=-8,
∴k=ab=-40.
点评 本题考查了平行四边形的性质和反比例函数图象上点的坐标特征.解题的难点是找到点A、B的坐标的横纵坐标的差与点C、D坐标的横纵坐标的差分别相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
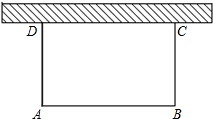 如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).
如图,用长为30米的篱笆围成一个一边靠墙的矩形养鸡场ABCD,已知墙长14m,设边AD的长为x(m),矩形ABCD的面积为y(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
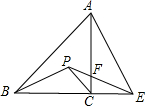 如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.
如图,在等腰Rt△ABC中,AC=BC,E为BC的延长线上一点,连接AE,若线段AE的中垂线交∠ABC的平分线于点P,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
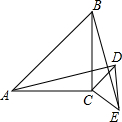 如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.
如图,△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD、BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
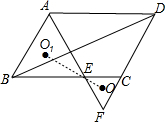 如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心
如图,在?ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、△ABE的外心查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.
如图,在?ABCD中,有下列四个条件:①AC=AD;②BA=BC;③∠ABC=90°;④AC=BD.添加其中的一个条件后,还不能使?ABCD成为菱形,则所添加的条件是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com