[题目]二次函数(a≠0)的图象如图所示.则下列命题中正确的是( )A. a ＞b＞cB. 一次函数y=ax +c的图象不经第四象限C. m(am+b)+b＜a(m是任意实数)D. 3b+2c＞0 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】二次函数（a≠0）的图象如图所示，则下列命题中正确的是（　　）

A. a ＞b＞c

B. 一次函数y=ax +c的图象不经第四象限

C. m（am+b）+b＜a（m是任意实数）

D. 3b+2c＞0

【答案】D

【解析】解：A．由二次函数的图象开口向上可得a＞0，由抛物线与y轴交于x轴下方可得c＜0，由x=﹣1，得出=﹣1，故b＞0，b=2a，则b＞a＞c，故此选项错误；

B．∵a＞0，c＜0，∴一次函数y=ax+c的图象经一、三、四象限，故此选项错误；

C．当x=﹣1时，y最小，即a﹣b﹣c最小，故a﹣b﹣c＜am2+bm+c，即m（am+b）+b＞a，故此选项错误；

D．由图象可知x=1，a+b+c＞0①，∵对称轴x=﹣1，当x=1，y＞0，∴当x=﹣3时，y＞0，即9a﹣3b+c＞0②

①+②得10a﹣2b+2c＞0，∵b=2a，∴得出3b+2c＞0，故选项正确；

故选D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】下列各数中，是不等式 x＞1的解的是（）

A.﹣2B.0C.1D.3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】和数轴上的点一一对应的是（）

A.有理数B.无理数C.实数D.整数和分数

查看答案和解析>>

科目：初中数学 来源： 题型：

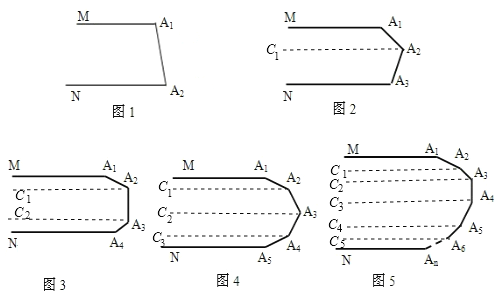
【题目】(1) 如图1，MA1∥NA2，则∠A1+∠A2=_________度．

如图2，MA1∥NA3，则∠A1+∠A2+∠A3=_________ 度．

如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4=_________度．

如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5=_________度．

如图5，MA1∥NAn，则∠A1+∠A2+∠A3+…+∠An=_________ 度．

(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°，求∠BFD的度数.

【答案】（1） 180； 360； 540；720；180（n-1）；（2）140°.

【解析】试题分析：（1）首先过各点作MA 1 的平行线，由MA 1 ∥NA 2 ，可得各线平行，根据两直线平行，同旁内角互补，即可求得答案；

（2）由（1）中的规律可得∠ABE+∠E+∠CDE=360°，所以∠ABE+∠CDE=360°-80°=280°，又因为BF、DF平分∠ABE和∠CDE，所以∠FBE+∠FDE=140°，又因为四边形的内角和为360°，进而可得答案．

试题解析：（1）如图1，

∵MA 1 ∥NA 2 ，

∴∠A 1 +∠A 2 =180°．

如图2，过点A 2 作A 2 C 1 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 3 =180°，

∴∠A 1 +∠A 2 +∠A 3 =360°．

如图3，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 4 =180°，

∴∠A 1 +∠A 2 +∠A 3 +∠A 4 =540°．

如图4，过点A 2 作A 2 C 1 ∥A 1 M，过点A 3 作A 3 C 2 ∥A 1 M，

∵MA 1 ∥NA 3 ，

∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ，

∴∠A 1 +∠A 1 A 2 C 1 =180°，∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°，∠C 2 A 3 A 4 +∠A 3 A 4 C 3 =180°，∠C 3 A 4 A 5 +∠A 5 =180°，

∴∠A 1 +∠A 2 +∠A 3 +∠A 4 +∠A 5 =720°；

从上述结论中你发现了规律：如图5，MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度，

故答案为：180，360，540，720，180（n-1）；

（2）由（1）可得∠ABE+∠E+∠CDE=360°，

∵∠E=80°，

∴∠ABE+∠CDE=360°-80°=280°，

又∵BF、DF平分∠ABE和∠CDE，

∴∠FBE+∠FDE=140°，

∵∠FBE+∠E+∠FDE+∠BFD=360°，

∴∠BFD=360°-80°-140°=140°．

【点睛】本题考查了平行线的性质：两直线平行，同旁内角互补、四边形的内角和是360°，解题的关键是，（1）小题正确添加辅助线，发现规律：MA 1 ∥NA n ，则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180（n-1）度；（2）小题能应用（1）中发现的规律.

【题型】解答题
【结束】
28

【题目】已知如图1，线段AB、CD相交于点O，连结AC、BD，我们把形如图1的图形称之为“8字形”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥聪明才智，解决以下问题：

(1)在图1中，请写出∠A、∠B、∠C、∠D之间的数量关系，并说明理由；

(2)仔细观察，在图2中“8字形”的个数有个；

(3)在图2中，若∠B＝76°，∠C＝80°，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N利用(1)的结论，试求∠P的度数；

(4)在图3中，如果∠B和∠C为任意角，并且AP和DP分别是∠CAB和∠BDC的三等分线，即∠PAO＝∠CAO， ∠BDP＝∠BOD，那么∠P与∠C、∠B之间存在的数量关系是（直接写出结论即可）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图 (1)，已知△ABC是等边三角形，以BC为直径的⊙O交AB、AC于D、E.求证：

(1)△DOE是等边三角形.

(2)如图(2)，若∠A=60°，AB≠AC，则(1)中结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】若关于a，b的多项式3(a2﹣2ab﹣b2)﹣(a2+mab+2b2)中不含有ab项，则m=_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某商场用36000元购进甲、乙两种商品，销售完后共获利6000元．其中甲种商品每件进价120元，售价138元；乙种商品每件进价100元，售价120元．

（1）该商场购进甲、乙两种商品各多少件？

（2）商场第二次以原进价购进甲、乙两种商品，购进乙种商品的件数不变，而购进甲种商品的件数是第一次的2倍，甲种商品按原售价出售，而乙种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于8160元，乙种商品最低售价为每件多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

请你根据统计图解答下列问题：

（1）参加比赛的学生共有____名；

（2）在扇形统计图中，m的值为____，表示“D等级”的扇形的圆心角为____度；

（3）组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在四边形ABCD中，∠A+∠B=200°，作∠ADC、∠BCD的平分线交于点O1称为第1次操作，作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作，作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作，…，则第5次操作后∠CO5D的度数是_____．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学