
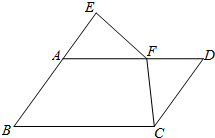
 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC. 科目:初中数学 来源: 题型:解答题
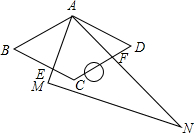 在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.
在菱形ABCD中,∠BAD=120°.现将-块含60°角的直角三角尺AMN(其中∠NAM=60°.)叠放在菱形上.然后将三角尺绕点A旋转.在旋转过程中.设AM交边BC于点E,AN交边CD于点F.那么BE+DF与AB有怎样的数量关系?请你通过动手操作.度量、猜想、验证等方法进行探索.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
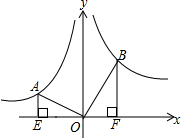 如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.
如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
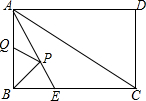 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵($\sqrt{a}-\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}+b≥0$,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com