
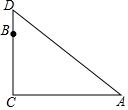
 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米. 分析 由题意知AD+DB=BC+CA,设BD=x,则AD=30-x,且在直角△ACD中CD2+CA2=AD2,代入勾股定理公式中即可求x的值,树高CD=(10+x)米即可.
解答 解:由题意知AD+DB=BC+CA,且CA=20米,BC=10米,
设BD=x,则AD=30-x,
∵在Rt△ACD中:CD2+CA2=AD2,
即(30-x)2=(10+x)2+202,
解得x=5米,故树高为CD=10+x=15米,
答:树高为15米.
故答案为:15.
点评 本题考查了勾股定理在实际生活中的应用,本题中找到AD+DB=BC+CA的等量关系,并根据勾股定理CD2+CA2=AD2求解是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
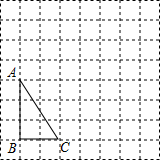 如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.
如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB=4cm.
如图,已知线段AB=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
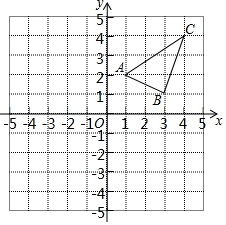 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(2)(3)(4) | B. | (2)(3)(4)(5) | C. | (1)(2)(3)(5) | D. | (1)(2)(4)(5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com