
已知二次函数y=x2–kx+k–1(k>2).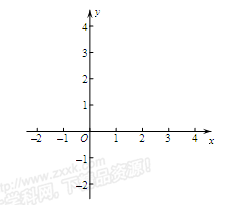
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若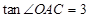 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与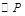 相离、相切、相交.
相离、相切、相交.
(1)证明详见解析;(2) ;(3)当
;(3)当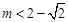 或
或 时,x轴与
时,x轴与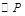 相离.;
相离.;
当 或
或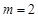 或
或 时,x轴与
时,x轴与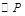 相切; 当
相切; 当 或
或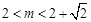 时,x轴与
时,x轴与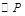 相交.
相交.
解析试题分析:(1)令y=0,得到一个关于字母x的一元二次方程,求出此方程的判别式的值为 ,根据k>2,可得
,根据k>2,可得
 ,即可得到答案.
,即可得到答案.
(2)令 ,有
,有 ;解得:
;解得: . 根据k的取值以及点A、B的位置确定
. 根据k的取值以及点A、B的位置确定 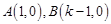 ;由抛物线与y轴交于点C得:
;由抛物线与y轴交于点C得: ;根据Rt
;根据Rt 中∠OAC的正切值求得k的取值,进而可得抛物线的表达式.(3)根据直线与圆的位置关系是由圆心到直线的距离和圆的半径确定的,当⊙P与x轴相切时,即y=±1;根据相切时m的取值即可作出判断,注意分类讨论.
中∠OAC的正切值求得k的取值,进而可得抛物线的表达式.(3)根据直线与圆的位置关系是由圆心到直线的距离和圆的半径确定的,当⊙P与x轴相切时,即y=±1;根据相切时m的取值即可作出判断,注意分类讨论.
试题解析:
(1)证明:∵
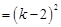 ,
,
又∵ ,
,
∴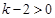 .
.
∴ 即
即 .
.
∴抛物线y = x2 – kx + k - 1与x轴必有两个交点.
(2) 解:∵抛物线y = x2 – kx + k -1与x轴交于A、B两点,
∴令 ,有
,有 .
.
解得: .
.
∵ ,点A在点B的左侧,
,点A在点B的左侧,
∴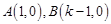 .
.
∵抛物线与y轴交于点C,
∴ .
.
∵在Rt 中,
中, 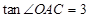 ,
,
∴ , 解得
, 解得 .
.
∴抛物线的表达式为 .
.
(3)解:当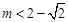 或
或 时,x轴与
时,x轴与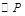 相离.
相离.
当 或
或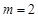 或
或 时,x轴与
时,x轴与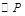 相切.
相切.
当 或
或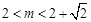 时,x轴与
时,x轴与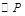 相交.
相交.
考点:1、根的判别式;2、求二次函数的解析式;3、直线与圆的位置关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:抛物线 与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
(1)求此二次函数的解析式;
(2)写出点C的坐标________,顶点D的坐标为__________;
(3)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式;
(4)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,如果存在,请直接写出所有满足条件的E点的坐标__________________________________(不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数 .
.
(1)若点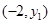 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”);
(2)如图,此二次函数的图象经过点 ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3).
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请求出出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
鄞州区有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类 野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售.
(1)设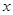 天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
天后每千克该野生菌的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批野生菌一次性出售,设这批野生菌的销售总额为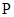 元,试写出
元,试写出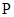 与x之间的函数关系式;
与x之间的函数关系式;
(3)李经理将这批野生菌存放多少天后出售可获得最大利润 元?
元?
(利润=销售总额-收购成本-各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,销售单价每提高1元,销售量相应减少10个.
(1)设销售单价提高x元(x为正整数),写出每月销售量y(个)与x(元)之间的函数关系式;
(2)假设这种篮球每月的销售利润为w元,试写出w与x之间的函数关系式,并通过配方讨论,当销售单价定为多少元时,每月销售这种篮球的利润最大,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
(1)求抛物线的解析式;
(2)判断△ABC的形状,说出△ABC外接圆的圆心位置,并求出圆心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com