
如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3).
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为10,请求出出点P的坐标.
(1)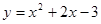 ;(2)(-4,5)或(2,5)
;(2)(-4,5)或(2,5)
解析试题分析:(1)利用待定系数法把A(1,0),C(0,-3)代入二次函数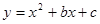 中,即可算出b、c的值,进而得到函数的解析式;
中,即可算出b、c的值,进而得到函数的解析式;
(2)首先求出A、B两点坐标,再算出AB的长,再设P(m,n),根据△ABP的面积为10可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标.
试题解析:(1)∵二次函数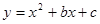 过点A(1,0),C(0,-3),
过点A(1,0),C(0,-3),
∴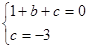 ,解得
,解得
∴二次函数的解析式为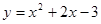 ;
;
(2)∵当 时,
时, ,解得
,解得 ,
,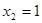 ;
;
∴A(1,0),B(-3,0),
∴AB=4,
设P(m,n),
∵△ABP的面积为10,
∴ •AB•|n|=10,解得
•AB•|n|=10,解得
当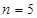 时,
时, ,解得
,解得 或2,
或2,
∴P(-4,5)(2,5);
当 时,
时, ,方程无解,
,方程无解,
故P(-4,5)或(2,5).
考点:1.待定系数法求二次函数解析式;2.二次函数的性质


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:解答题
二次函数 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程 的两个根.
的两个根.
(2)写出不等式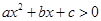 的解集.
的解集.
(3)写出 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围.
的取值范围.
(4)若方程 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,平面直角坐标系中,以点C(2,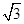 )为圆心,以2为半径的圆与
)为圆心,以2为半径的圆与 轴交于A、B两点.
轴交于A、B两点.
(1)求A、B两点的坐标;
(2)若二次函数 的图象经过点A、B,试确定此二次函数的解析式.
的图象经过点A、B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数y=x2–kx+k–1(k>2).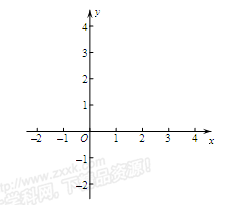
(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若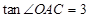 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与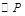 相离、相切、相交.
相离、相切、相交.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数y1=ax2+bx-3的图象经过点A(2,-3),B(-1,0),与y轴交于点C,与x轴另一交点交于点D.
(1)求二次函数的解析式;
(2)求点C、点D的坐标;
(3)若一条直线y2,经过C、D两点,请直接写出y1>y2时, 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商品的进价为每千克40元,销售单价与月销售量的关系如下表(每千克售价不能高于65元):
| 销售单价(元) | 50 | 53 | 56 | 59 | 62 | 65 |
| 月销售量(千克) | 420 | 360 | 300 | 240 | 180 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表表示:
| 等级(x级) | 一级 | 二级 | 三级 | … |
| 生产量(y台/天) | 78 | 76 | 74 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;(6分)
(2)将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;(4分)
(3)设过点E的直线交AB边于点P,交CD边于点Q.问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由. (4分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com