
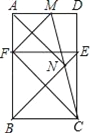
【题目】已知:矩形ABCD内一点N,△ANB为等腰直角三角形,连结BN、CN并延长分别交DC,AD于点E,M,在AB上截取BF=EC,连接MF.
(1)求证:四边形FBCE为正方形;
(2)求证:MN=NC;
(3)若S△FMC:S正方形FBCE=2:3,求BN:MD的值.
【答案】(1)证明见解析;(2)证明见解析;(3)BN:MD=![]() .
.
【解析】试题分析:(1)先证明四边形![]() 为矩形,再利用
为矩形,再利用![]() 为等腰直角三角形,证明
为等腰直角三角形,证明![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,所以四边形
,所以四边形![]() 为正方形;
为正方形;
(2)作辅助线,构建全等三角形,证明![]() ≌
≌![]() ,得
,得![]() ,再利用平行线分线段成比例定理可得
,再利用平行线分线段成比例定理可得![]() 则
则![]()
(3)设![]() 表示出
表示出![]() 和S正方形FBCE,并根据S△FMC:S正方形FBCE=2:3,依次计算出
和S正方形FBCE,并根据S△FMC:S正方形FBCE=2:3,依次计算出![]() 的长,最后得结论.
的长,最后得结论.
试题解析:(1)如图1,∵四边形ABCD为矩形,
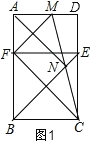
∴AB∥CD,![]()
∴BF∥EC,
∵BF=EC,
∴四边形FBCE为矩形,
∵△ANB为等腰直角三角形,
![]()
![]()
∴△BEC为等腰直角三角形,
∴BC=CE,
∴四边形FBCE为正方形;
(2)如图2,过N作GH⊥BC,交BC于H,AD于G,则GH⊥AD,
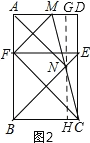
![]()
∴△BHN≌△AGN,
∴NG=NH,
∵AD∥BC,
∴![]()
∴MN=NC;
(3)如图2,设BF=1,则S正方形FBCE=1,![]() ,
,
∵FO=OC,MN=NC,
∴ON∥FM,
![]()
![]()
由于S△FMC:S正方形FBCE=2:3,
即![]()
![]()
![]()
![]()
∴△AFM是等腰直角三角形,
![]()
![]()
![]()
![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
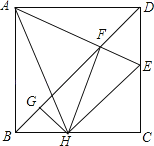
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
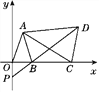
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了点做圆周运动的一个动画游戏,如上图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=![]() t2+
t2+![]() t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
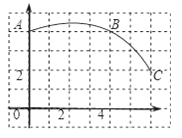
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)本次接受调查的跳水运动员人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com