
【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( )
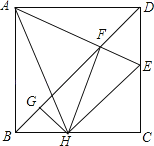
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】D
【解析】(1)如图1,连接FC,延长HF交AD于点L,
∵在正方形ABCD中,∠ADF=∠CDF=45°,AD=CD,DF=DF,
∴△ADF≌△CDF,
∴FC=AF,∠ECF=∠DAF,
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°,
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC,
∴FH=AF;
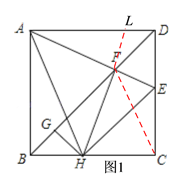
(2)如图1,∵FH⊥AE,FH=AF,
∴∠HAE=45°;
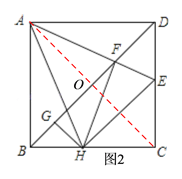
(3)如图2,连接AC交BD于点O,则由正方形的性质可得:BD=2OA,
∵ HF⊥AE,HG⊥BD,
∴∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG;
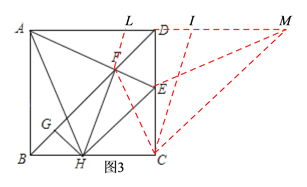
(4)延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,
∴∠IMC=∠ECM=45°,
由已知条件可得:∠DEM=∠DEA=∠FHC=∠DIC,由此可得∠MEC=∠CIM,
又∵MC=CM,
∴△MEC≌△CIM,
∴CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=8.
∴△CEH的周长为8,为定值.
故(1)(2)(3)(4)结论都正确.


科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC边为直径,作⊙O,交AB于点D(保留作图痕迹,标上相应的字母,可不写作法);
(2)连结DE,求证:DE为⊙O的切线;
(3)若AD=4,BD=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字1,2,3,4.第一次从袋中随机地抽出一张卡片,把其上的数字记为横坐标x,然后把卡片放回袋中,搅匀后第二次再随机地从中抽出一张,把其上的数字记为纵坐标y.
(1)用树状图或列表法把所有可能的点表示出来;
(2)求所得的点在直线y=﹣x+5的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
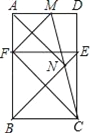
【题目】已知:矩形ABCD内一点N,△ANB为等腰直角三角形,连结BN、CN并延长分别交DC,AD于点E,M,在AB上截取BF=EC,连接MF.
(1)求证:四边形FBCE为正方形;
(2)求证:MN=NC;
(3)若S△FMC:S正方形FBCE=2:3,求BN:MD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com