
| 汽车行驶时间t/h | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q/L | 100 | 94 | 88 | 82 | … |
分析 (1)由表格可知,开始油箱中的油为100L,每行驶1小时,油量减少6L,据此可得t与Q的关系式;
(2)求汽车行驶5h后,油箱中的剩余油量即是求当t=5时,Q的值;
(3)贮满48L汽油的汽车,理论上最多能行驶几小时即是求当Q=0时,t的值.
解答 解:(1)Q=100-6t;
(2)当t=5时,Q=100-6×5=70,
答:汽车行驶5h后,油箱中的剩余油量是70L;
(3)当Q=48时,48=100-6t
解得:t=$\frac{26}{3}$,
100×$\frac{26}{3}$=$\frac{2600}{3}$km.
答:该车最多能行驶$\frac{2600}{3}$km;
点评 本题考查了一次函数的应用,关键是求函数关系式.注意贮满100L汽油的汽车,最多行驶的时间就是油箱中剩余油量为0时的t的值.


科目:初中数学 来源: 题型:解答题
 阅读:
阅读:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | -$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.
如图,有一张直角三角形纸片,两直角边AC=7cm,BC=11cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为$\frac{36}{11}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
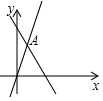 如图,已知函数y=3x和y=ax+5的图象相交于点A(n,3),则不等式3x>ax+5的解集为( )
如图,已知函数y=3x和y=ax+5的图象相交于点A(n,3),则不等式3x>ax+5的解集为( )| A. | x<0 | B. | x<1 | C. | x>1 | D. | x>3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com