
 如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题: ,
, x,
x, ×48=12km;
×48=12km;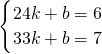 ,
,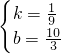 ,
, x+
x+ ,
, x+
x+ =5,
=5, ,
,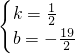 ,
, x-
x- ,
,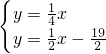 ,
,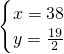 ,
, x,12;(2)20~33min;(3)38.
x,12;(2)20~33min;(3)38.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 变化的图象.下面几个结论:
变化的图象.下面几个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
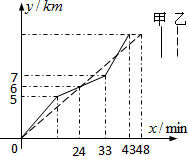 如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.
如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.查看答案和解析>>
科目:初中数学 来源:2007年福建省福州市福清市临江中学中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com