
 如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.
如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 4 |
|
|
| 1 |
| 2 |
| 19 |
| 2 |
|
|


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
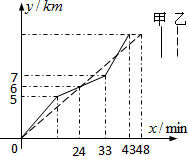 如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
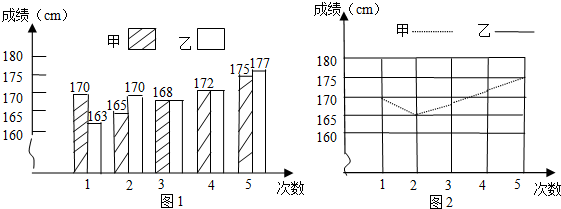
. |
| x甲 |
| S | 2 甲 |
. |
| x乙 |
| S | 2 乙 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
如图表示甲、乙两名赛车选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源:2007年福建省福州市福清市临江中学中考数学模拟试卷(解析版) 题型:解答题
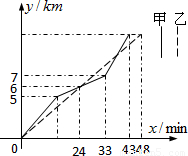
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
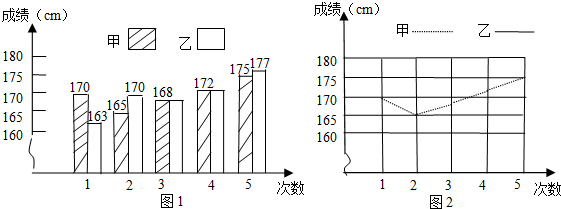
 =170,
=170,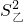 =11.6,试求:
=11.6,试求: 与
与  ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com