
 如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )
如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 9 | D. | 3$\sqrt{3}$ |
分析 根据线段垂直平分线上的点到线段两端距离相等可得AD=BD,可得∠DAE=30°,易得∠ADC=60°,∠CAD=30°,则AD为∠BAC的角平分线,由角平分线的性质得DE=CD=3,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2DE,得结果.
解答 解:∵DE是AB的垂直平分线,
∴AD=BD,
∴∠DAE=∠B=30°,
∴∠ADC=60°,
∴∠CAD=30°,
∴AD为∠BAC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=CD=3,
∵∠B=30°,
∴BD=2DE=6,
∴BC=9,
故选C.
点评 本题主要考查了垂直平分线的性质,角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
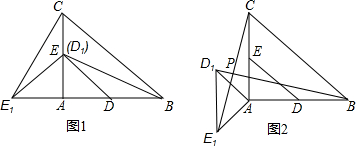
 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且$\widehat{DE}$=$\widehat{BE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3mn)2=-6m2n2 | B. | 4x4+2x4+x4=6x4 | C. | (xy)2÷(-xy)=-xy | D. | (a-b)(-a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a2)3=6a6 | B. | -a2b2•3ab3=-3a2b5 | ||
| C. | $\frac{{a}^{2}-1}{a}$•$\frac{1}{a+1}$=-1 | D. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com