Question

14．如图，将平行四边形ABCD沿边AB的平行线EF对折，∠DEF=50°，则∠BFC的度数是80°．

Answer 1

分析 延长AE到D′，使AE=ED′，延长BF到C′，使BF=FC′，连接D′C′，由折叠可得∠D′EF=′DEF=50°，根据平角定义可得∠AED的度数，然后利用平行线的性质可得∠BFC的度数．

解答 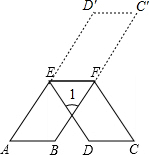解：∵延长AE到D′，使AE=ED′，延长BF到C′，使BF=FC′，连接D′C′，
由折叠可得∠D′EF=′DEF=50°，
∴∠AED=180°-50°×2=80°，
∵四边形AD′C′B是平行四边形，
∴AE∥BF，
∵AB∥EF，
∴四边形ABFE是平行四边形，
∴∠1=∠AED=80°，EF=AB，
∵四边形AD′C′B是平行四边形，
∴ED∥FC，
∴∠1=∠BFC=80°，
故答案为：80°．

点评 此题主要考查了平行四边形的性质，以及图形的折叠，关键是掌握平行四边形的对边相等且平行．