
 ШчЭМЃЌУцЛ§ЮЊ1ЕФЕШбќжБНЧЁїOA1A2ЃЌЁЯOA2A1=90ЁуЃЌЧвOA2ЮЊаББпдкЁїOA1A2ЃЌЭтзїЕШбќжБНЧЁїOA2A3ЃЌвдOA3ЮЊаББпдкЁїOA2A3ЃЌЭтзїЕШбќжБНЧЁїOA3A4ЃЌвдOA4ЮЊаББпдкЁїOA3A4ЃЌЭтзїЕШбќжБНЧЁїOA4A5ЃЌЁСЌНгA1A3ЃЌA3A5ЃЌA5A7ЃЌЁЗжБ№гыOA2ЃЌOA4ЃЌOA6ЃЌЁНЛгкЕуB1ЃЌB2ЃЌB3ЃЌЁАДДЫЙцТЩМЬајЯТШЅЃЌМЧЁїOB1A3ЕФУцЛ§ЮЊS1ЃЌЁїOB2A5ЕФУцЛ§ЮЊS2ЃЌЁїOB3A7ЕФУцЛ§ЮЊS3ЃЌЁЁїOBnA2n+1ЕФУцЛ§ЮЊSnЃЌдђSn=$ЃЈ\frac{1}{4}ЃЉ^{n-1}ЁС\frac{1}{3}$ЃЈгУКЌе§ећЪ§nЕФЪНзгБэЪОЃЉЃЎ
ШчЭМЃЌУцЛ§ЮЊ1ЕФЕШбќжБНЧЁїOA1A2ЃЌЁЯOA2A1=90ЁуЃЌЧвOA2ЮЊаББпдкЁїOA1A2ЃЌЭтзїЕШбќжБНЧЁїOA2A3ЃЌвдOA3ЮЊаББпдкЁїOA2A3ЃЌЭтзїЕШбќжБНЧЁїOA3A4ЃЌвдOA4ЮЊаББпдкЁїOA3A4ЃЌЭтзїЕШбќжБНЧЁїOA4A5ЃЌЁСЌНгA1A3ЃЌA3A5ЃЌA5A7ЃЌЁЗжБ№гыOA2ЃЌOA4ЃЌOA6ЃЌЁНЛгкЕуB1ЃЌB2ЃЌB3ЃЌЁАДДЫЙцТЩМЬајЯТШЅЃЌМЧЁїOB1A3ЕФУцЛ§ЮЊS1ЃЌЁїOB2A5ЕФУцЛ§ЮЊS2ЃЌЁїOB3A7ЕФУцЛ§ЮЊS3ЃЌЁЁїOBnA2n+1ЕФУцЛ§ЮЊSnЃЌдђSn=$ЃЈ\frac{1}{4}ЃЉ^{n-1}ЁС\frac{1}{3}$ЃЈгУКЌе§ећЪ§nЕФЪНзгБэЪОЃЉЃЎ ЗжЮі ЯШИљОнЕШбќжБНЧШ§НЧаЮЕФЖЈвхЧѓГіЁЯA1OA3=ЁЯOA3A2=90ЁуЃЌЕУA2A3ЁЮOA1ЃЌИљОнЭЌЕзЕШИпЕФСНИіШ§НЧаЮЕФУцЛ§ЯрЕШЕУЃК${S}_{Ёї{A}_{1}{A}_{2}O}$=${S}_{Ёї{A}_{1}{A}_{3}O}$ЃЌЫљвд${S}_{ЁїO{A}_{3}{B}_{1}}$=${S}_{Ёї{A}_{1}{A}_{2}{B}_{1}}$ЃЌЭЌРэЕУЃКA4A5ЁЮA3OЃЌЭЌРэЕУЃК${S}_{ЁїO{B}_{2}{A}_{5}}$=${S}_{Ёї{A}_{3}{A}_{4}{B}_{2}}$ЃЌИљОнвбжЊЕФ${S}_{ЁїO{A}_{1}{A}_{2}}$=1ЃЌЧѓЖдгІЕФжБНЧБпКЭаББпЕФГЄЃКOA2=A1A2=$\sqrt{2}$ЃЌA2A3=OA3=1ЃЌOA1=2ЃЌВЂРћгУЦНааЯрЫЦжЄУїЁїA2B1A3ЁзЁїOB1A1ЃЌСаБШР§ЪНПЩвдЧѓA2B1=$\frac{\sqrt{2}}{3}$ЃЌИљОнУцЛ§ЙЋЪНМЦЫуS1=$\frac{1}{3}$ЃЌЭЌРэЕУЃКS2=$\frac{1}{4}$ЁС$\frac{1}{3}$ЃЌДгЖјЕУГіЙцТЩЃКSn=$\frac{1}{4}$Sn-1=$ЃЈ\frac{1}{4}ЃЉ^{n-1}$ЁС$\frac{1}{3}$ЃЎ
НтД№ НтЃКЁпЁїOA1A2ЁЂЁїOA2A3ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯA1OA2=ЁЯA2OA3=45ЁуЃЌ
ЁрЁЯA1OA3=ЁЯOA3A2=90ЁуЃЌ
ЁрA2A3ЁЮOA1ЃЌ
Ёр${S}_{Ёї{A}_{1}{A}_{2}O}$=${S}_{Ёї{A}_{1}{A}_{3}O}$ЃЈЭЌЕзЕШИпЃЉЃЌ
Ёр${S}_{ЁїO{A}_{3}{B}_{1}}$+${S}_{ЁїO{A}_{1}{B}_{1}}$=${S}_{ЁїO{A}_{1}{B}_{1}}$+${S}_{Ёї{A}_{1}{A}_{2}{B}_{1}}$ЃЌ
Ёр${S}_{ЁїO{A}_{3}{B}_{1}}$=${S}_{Ёї{A}_{1}{A}_{2}{B}_{1}}$ЃЌ
ЭЌРэЕУЃКA4A5ЁЮA3OЃЌ
${S}_{ЁїO{B}_{2}{A}_{5}}$=${S}_{Ёї{A}_{3}{A}_{4}{B}_{2}}$ЃЌ
Ёп${S}_{ЁїO{A}_{1}{A}_{2}}$=1ЃЌ
Ёр$\frac{1}{2}$OA2•A1A2=1ЃЌ
ЁпOA2=A1A2ЃЌ
ЁрOA2=A1A2=$\sqrt{2}$ЃЌ
ЁрA2A3=OA3=1ЃЌOA1=2ЃЌ
ЁпA2A3ЁЮOA1ЃЌ
ЁрЁїA2B1A3ЁзЁїOB1A1ЃЌ
Ёр$\frac{{A}_{2}{A}_{3}}{O{A}_{1}}$=$\frac{{A}_{2}{B}_{1}}{O{B}_{1}}$=$\frac{1}{2}$ЃЌ
ЁпA2O=$\sqrt{2}$ЃЌ
ЁрA2B1=$\frac{\sqrt{2}}{3}$ЃЌ
ЁрS1=${S}_{ЁїO{A}_{3}{B}_{1}}$=${S}_{Ёї{A}_{1}{A}_{2}{B}_{1}}$=$\frac{1}{2}$A1A2•A2B1=$\frac{1}{2}$ЁС$\sqrt{2}$ЁС$\frac{\sqrt{2}}{3}$=$\frac{1}{3}$ЃЌ
ЭЌРэЕУЃКOA4=A3A4=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ЃЌA4A5=$\frac{1}{2}$ЃЌ
ЁрЁїA4A5B2ЁзЁїOA3B2ЃЌ
Ёр$\frac{{A}_{4}{B}_{2}}{O{B}_{2}}$=$\frac{{A}_{4}{A}_{5}}{O{A}_{3}}$=$\frac{\frac{1}{2}}{1}$=$\frac{1}{2}$ЃЌ
ЁрA4B2=$\frac{1}{3}O{A}_{4}$=$\frac{1}{3}$ЁС$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{6}$ЃЌ
ЁрS2=${S}_{ЁїO{A}_{5}{B}_{2}}$=${S}_{Ёї{A}_{3}{A}_{4}{B}_{2}}$=$\frac{1}{2}$ЁС$\frac{\sqrt{2}}{2}$ЁС$\frac{\sqrt{2}}{6}$=$\frac{1}{4}$ЁС$\frac{1}{3}$ЃЌ
ЫљвдЕУГіЙцТЩЃКSn=$\frac{1}{4}$Sn-1=$ЃЈ\frac{1}{4}ЃЉ^{n-1}$ЁС$\frac{1}{3}$ЃЌ
ЙЪД№АИЮЊЃК$ЃЈ\frac{1}{4}ЃЉ^{n-1}$ЁС$\frac{1}{3}$ЃЎ
ЕуЦР БОЬтПМВщСЫЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌЙДЙЩЖЈРэЃЌЯрЫЦШ§НЧаЮЕФаджЪКЭХаЖЈвдМАШ§НЧаЮУцЛ§ЕФМЦЫуЮЪЬтЃЌБШНЯИДдгЃЌЪщаДЪБаЁЯТБъНЯЖрЃЌвЊШЯецЪщаДЃЌЯШИљОнЕШбќжБНЧШ§НЧаЮЕФУцЛ§ЧѓИїБпЕФГЄЃЌРћгУЭЌЕзЕШИпЕФШ§НЧаЮУцЛ§ЯрЕШНЋЫљЧѓЕФШ§НЧаЮНјаазЊЛЏЃЌДгЖјНтОіЮЪЬтЃЌВЂЗЂЯжЙцТЩЃЎ


 ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 3cm | BЃЎ | 4cm | CЃЎ | 7cm | DЃЎ | 9cm |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2гы|-2| | BЃЎ | -2гы$\sqrt{ЃЈ-2ЃЉ^{2}}$ | CЃЎ | -2гы-$\frac{1}{2}$ | DЃЎ | -2гы$\root{3}{-8}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЛжИДдМл | BЃЎ | НЕМл4% | CЃЎ | ЬсМл4% | DЃЎ | вдЩЯЖМВЛЖд |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
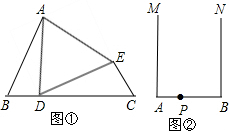
 ШчЭМЃЌдкЁїABCжаЃЌЁЯABE=2ЁЯCЃЌADЪЧЁЯBACЕФЦНЗжЯпЃЌBEЁЭADЃЌДЙзуЮЊE
ШчЭМЃЌдкЁїABCжаЃЌЁЯABE=2ЁЯCЃЌADЪЧЁЯBACЕФЦНЗжЯпЃЌBEЁЭADЃЌДЙзуЮЊEВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌдкГЄКЭПэЗжБ№ЮЊmЃЌnЕФГЄЗНаЮЬњЦЄЕФЫФИіНЧЖММєШЅвЛИіБпГЄЮЊxЕФе§ЗНаЮЃЈ2xЃМnЃМmЃЉЃЌелЕўКѓЃЌзіГЩвЛЮоИЧЕФКазгЃЌдђетИіГЄЗНЬхКазгЕФБэУцЛ§ЪЧmn-4x2ЃЎ
ШчЭМЃЌдкГЄКЭПэЗжБ№ЮЊmЃЌnЕФГЄЗНаЮЬњЦЄЕФЫФИіНЧЖММєШЅвЛИіБпГЄЮЊxЕФе§ЗНаЮЃЈ2xЃМnЃМmЃЉЃЌелЕўКѓЃЌзіГЩвЛЮоИЧЕФКазгЃЌдђетИіГЄЗНЬхКазгЕФБэУцЛ§ЪЧmn-4x2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
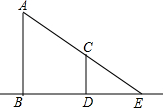 ШчЭМЃЌвбжЊаЁгуЭЌбЇЕФЩэИпЃЈCDЃЉЪЧ1.6УзЃЌЫ§гыЪїЃЈABЃЉдкЭЌвЛЪБПЬЕФгАзгГЄЗжБ№ЮЊDE=2УзЃЌBE=5УзЃЌФЧУДЪїЕФИпЖШAB=4УзЃЎ
ШчЭМЃЌвбжЊаЁгуЭЌбЇЕФЩэИпЃЈCDЃЉЪЧ1.6УзЃЌЫ§гыЪїЃЈABЃЉдкЭЌвЛЪБПЬЕФгАзгГЄЗжБ№ЮЊDE=2УзЃЌBE=5УзЃЌФЧУДЪїЕФИпЖШAB=4УзЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com