
【题目】如图,△ABC沿直线L对折后能与△ADC重合,且AB∥CD,下列选项正确的是( ) 
A.AB=CD,AO=OC
B.AB=BD,∠BAD=∠DCB
C.AB∥BC,BC=BD
D.OD=OB,∠CDB=∠BCD
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示为一个污水净化塔内部,污水从上方入口进入后,流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
AB长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
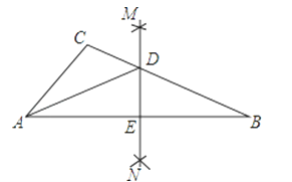
A. 3 B. 3.5 C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P; 
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,回答下列各题:
(1)图A中,共有____对对顶角;
(2)图B中,共有____对对顶角;
(3)图C中,共有____对对顶角;
(4)探究(1)--(3)各题中直线条数与对顶角对数之间的关系,若有n条直线相交于一点,则可形成________对对顶角;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1). 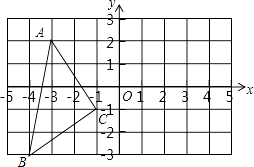
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1 , B1 , C1的坐标(直接写答案):A1;B1;C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.经过半径的端点并且垂直于这条半径的直线是这个圆的切线
B.平分弦的直径垂直于弦,并且平分弦所对的两条弧
C.90°的圆周角所对的弦是直径
D.如果两个圆周角相等,那么它们所对的弦相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com