
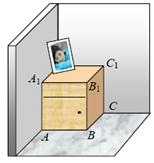
 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.分析 根据题意,先将长方体展开,再根据两点之间线段最短.
解答 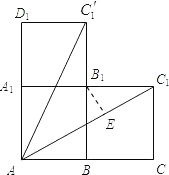 解:(1)如图,
解:(1)如图,
木柜的表面展开图是矩形ABC'1D1或ACC1A1.
故蚂蚁能够最快到达目的地的可能路径有如图的AC'1或AC1;
(2)蚂蚁沿着木柜表面矩形ABC'1D1爬过的路径AC'1的长是l1=$\sqrt{{4}^{2}+(4+5)^{2}}$.
蚂蚁沿着木柜表面矩形矩形AB1C1D爬过的路径AC1的长l1=$\sqrt{97}$,
蚂蚁沿着木柜表面ACC1A1爬过的路径AC1的长是l2=$\sqrt{(4+4)^{2}+{5}^{2}}$.
l1>l2,故最短路径的长是l2$\sqrt{89}$.
(3)作B1E⊥AC1于E,
∵∠C1EB1=∠C1A1A,∠A1C1A是公共角,
∴△AA1C1∽△B1EC1,
即$\frac{{B}_{1}E}{A{A}_{1}}$=$\frac{{B}_{1}{C}_{1}}{A{C}_{1}}$,
则B1E=$\frac{{B}_{1}{C}_{1}}{A{C}_{1}}$•AA1=$\frac{4}{\sqrt{89}}$•5=$\frac{20}{89}$为所求.
点评 此题考查了平面展开-最短路径问题,本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 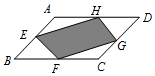 | B. | 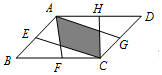 | ||
| C. | 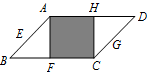 | D. | 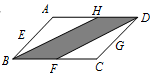 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
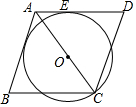 如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.
如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
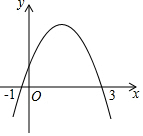 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a+b+c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com