
分析 根据一次函数图象上点的坐标特征确定两直线的交点坐标,然后根据函数图象交点坐标为两函数解析式组成的方程组的解选择答案.
解答 解:把(-1,a)代入y=2x得a=-2,
则直线y=2x与y=-x+b的交点为(-1,-2),
则方程组$\left\{\begin{array}{l}{y-2x=0}\\{y+x-b=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.


科目:初中数学 来源: 题型:解答题
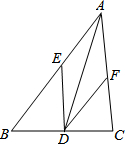 如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.
如图,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
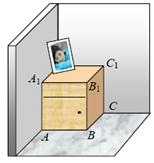 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
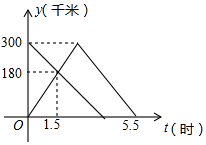 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com