
 如图所示,反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P,则称P为切点.若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )
如图所示,反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P,则称P为切点.若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )| A. | (-1,3) | B. | (3,-1) | C. | (1,3) | D. | (-3,1) |
分析 将一次函数解析式代入反比例函数解析式中,利用根的判别式△=0即可求出k值,取其负值,再联立两函数解析式成方程组,通过解方程组即可求出两函数图象的交点坐标.
解答 解:将y=kx+6代入y=$-\frac{k}{x}$中,
整理得:kx2+6x+k=0,
∵反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M,且k<0,
∴△=62-4k2=0,
解得:k=-3或k=3(舍去),
∴直线的解析式为y=-3x+6,反比例函数的解析式为y=$\frac{3}{x}$.
联立两函数解析式成方程组,
$\left\{\begin{array}{l}{y=-3x+6}\\{y=\frac{3}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,
∴当k<0时切点M的坐标为(1,3).
故选C.
点评 本题考查了反比例函数与一次函数的交点问题以及根的判别式,由两函数图象只有一个交点,利用根的判别式△=0找出k值是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:选择题
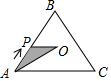 如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )| A. | 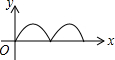 | B. | 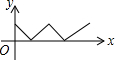 | C. | 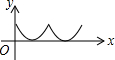 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
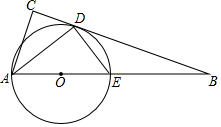 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是4 | D. | 方差是1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
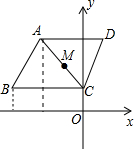 如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )| A. | (-2017,2) | B. | (-2017,-2) | C. | (-2018,-2) | D. | (-2018,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
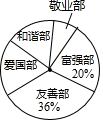 小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示.
小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示. | 福卡 | 和谐福 | 富强福 | 爱国福 | 友善福 | 敬业福 |
| 人数 | 21 | 20 | a | b | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com