
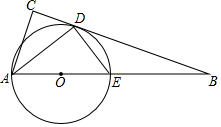
 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.分析 (1)连接OD,如图,证明∠2=∠BAD,加上∠DBE=∠ABD,则根据相似三角形的判定方法可判定△BDE∽△BAD,然后利用相似比可得到结论;
(2)先在Rt△BOD中利用余弦的定义得到cosB=$\frac{BD}{BO}$=$\frac{2\sqrt{2}}{3}$,设BD=2$\sqrt{2}$x,则BO=3x,利用勾股定理计算出OD=x,所以x=2,则BD=4$\sqrt{2}$,BO=6,然后根据平行线分线段成比例定理计算CD的长.
解答 (1)证明:连接OD,如图,
∵AD平分∠BAC,
∴∠4=∠BAD,
∵OA=OD,
∴∠OAD=∠1,
∴∠1=∠4,
∴AC∥OD,
∴∠ODB=∠C=90°,
即∠3+∠2=90°,
∵AE为直径,
∴∠ADE=90°,即∠1+∠3=90°,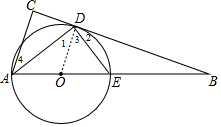
∴∠1=∠2,
∴∠2=∠BAD,
而∠DBE=∠ABD,
∴△BDE∽△BAD,
∴BD:BA=BE:BD,
∴BD2=BE•BA;
(2)∵AE=4,
∴OD=2,
在Rt△BOD中,cosB=$\frac{BD}{BO}$=$\frac{2\sqrt{2}}{3}$,
设BD=2$\sqrt{2}$x,则BO=3x,
∴OD=$\sqrt{(3x)^{2}-(2\sqrt{2}x)^{2}}$=x,
∴x=2,
∴BD=4$\sqrt{2}$,BO=6,
∵OD∥AC,
∴$\frac{BD}{CD}$=$\frac{BO}{OA}$,即$\frac{4\sqrt{2}}{CD}$=$\frac{6}{2}$,
∴CD=$\frac{4\sqrt{2}}{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,在应用相似三角形的性质时主要利用相似比计算线段的长或表示线段之间的关系.也考查了圆周角定理和平行线分线段成比例定理.


科目:初中数学 来源: 题型:解答题
 某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;
某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
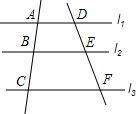 如图,若l1∥l2∥l3,则下列各式错误的是( )
如图,若l1∥l2∥l3,则下列各式错误的是( )| A. | $\frac{BC}{AC}$=$\frac{EF}{DF}$ | B. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | C. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | D. | $\frac{AB}{AC}$=$\frac{DE}{EF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
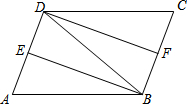 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
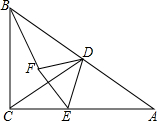 如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.
如图,在Rt△ABC中,∠C=90°,∠A=30°.点D是AB中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边三角形DEF,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P,则称P为切点.若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )
如图所示,反比例函数y=$\frac{1}{x}$与直线y=-x+2只有一个公共点P,则称P为切点.若反比例函数y=$-\frac{k}{x}$与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )| A. | (-1,3) | B. | (3,-1) | C. | (1,3) | D. | (-3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )| 甲 | 乙 | |
| 平均数 | 9 | 8 |
| 方差 | 1 | 1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com