
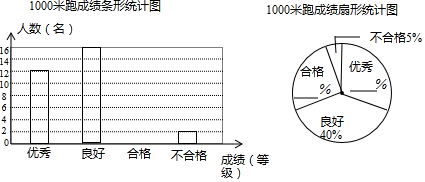
 甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
甲、乙、丙、丁四名射击运动员在选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )| 甲 | 乙 | |
| 平均数 | 9 | 8 |
| 方差 | 1 | 1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
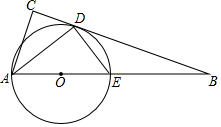 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
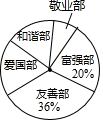 小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示.
小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示. | 福卡 | 和谐福 | 富强福 | 爱国福 | 友善福 | 敬业福 |
| 人数 | 21 | 20 | a | b | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
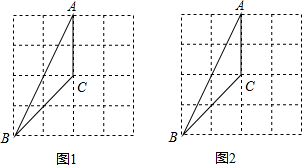
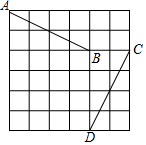 如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).
如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
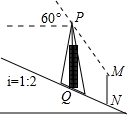 如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com