
 某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;
某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;分析 (1)观察图象,寻找规律即可解决问题;
(2)利用待定系数法即可解决问题;
(3)求出直线EF的解析式,解方程组求出点E坐标即可解决问题.
解答 解:(1)观察图象可知时间为20s、100s时,该食物的温度分别为50°C,62°C.
故答案为50,62.
(2)设直线DE的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{10k+b=35}\\{30k+b=65}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=20}\end{array}\right.$,
∴y=$\frac{3}{2}$x+20.
(3)设直线EF的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{90m+n=65}\\{100m+n=62}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{3}{10}}\\{n=92}\end{array}\right.$,
∴y=-$\frac{3}{10}$x+92,
由$\left\{\begin{array}{l}{y=-\frac{3}{10}x+92}\\{y=\frac{3}{2}x+20}\end{array}\right.$解得$\left\{\begin{array}{l}{x=40}\\{y=80}\end{array}\right.$,
∴x=40s时,食物的温度最高,最高温度是80°C.
点评 本题考查一次函数的应用、待定系数法等知识,解题的关键是灵活运用所学知识解决问题,学会利用方程组确定两个函数图象的交点坐标,属于中考常考题型.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
| 次数 | 牛奶(瓶) | 面包(个) | 总金额(元) |
| 第1次 | 30 | 50 | 430 |
| 第2次 | 20 | 60 | 420 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
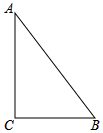 如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
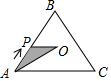 如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )| A. | 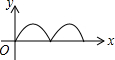 | B. | 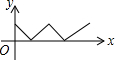 | C. | 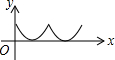 | D. | 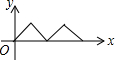 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
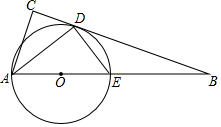 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com