
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
分析 (1)根据总利润=(甲的售价-甲的进价)×购进甲的数量+(乙的售价-乙的进价)×购进乙的数量代入列关系式,并化简;
(2)根据总成本≤9000列不等式即可求出x的取值,再根据函数的增减性确定其最值问题;
(3)把50<m<70分三种情况讨论:一次项x的系数大于0、等于0、小于0,根据函数的增减性得出结论.
解答 解:(1)y=80x+140(100-x)=-60x+14000.
80x+100(100-x)≤9000,
解得x≥50,
∴50≤x≤100.
(2)∵y=-60x+14000,50≤x≤100,
又∵-60<0,
∴x=50时,y有最大值,最大值=11000,
答:商场至少要购进50件甲商品,销售完这些商品.商场可获得的最大利润,最大利润为11000元.
(3)y=(80+m)x+140(100-x) (50≤x≤100),
y=(m-60)x+14000,
①当50<m<60时,m-60<0,y随x的增大而减小,
∴当x=50时,y有最大利润,
即商场应购进甲商品50件,乙商品50件,获利最大,
②当m=60时,m-60=0,y=28000,
即商场应购进甲商品的数量满足50≤x≤100的整数件时,获利最大,
③当60<m<70时,m-60>0,y随x的增大而增大,
∴当x=100时,y有最大利润,
即商场应购进甲商品100件,乙商品0件,获利最大.
点评 本题是一次函数和一元一次不等式的综合应用,属于销售利润问题,在此类题中,要明确售价、进价、利润的关系式:单件利润=售价-进价,总利润=单个利润×数量,商品利润率=商品利润/商品进价×100%;认真读题,弄清题中的每一个条件;对于最值问题,可利用一次函数的增减性来解决:形如y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:填空题
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
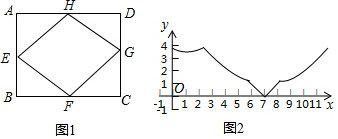
| A. | 点E | B. | 点F | C. | 点G | D. | 点H |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
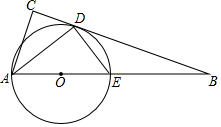 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
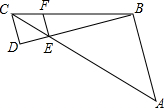 如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是4 | D. | 方差是1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
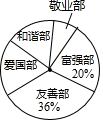 小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示.
小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示. | 福卡 | 和谐福 | 富强福 | 爱国福 | 友善福 | 敬业福 |
| 人数 | 21 | 20 | a | b | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
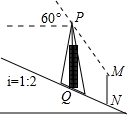 如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)
如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2$\sqrt{5}$米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com