
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
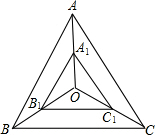 如图,点O是等边三角形ABC的中心,A1,B1,C1分别是OA,OB,OC的中点,则△A1BlCl与△ABC的位似比,位似中心分别是
如图,点O是等边三角形ABC的中心,A1,B1,C1分别是OA,OB,OC的中点,则△A1BlCl与△ABC的位似比,位似中心分别是查看答案和解析>>
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:047
如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,那么这两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位似中心.利用三角形的位似可以将一个三角形缩小或放大.
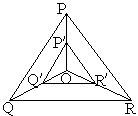
(1)选择:如图,点O是等边三角形PQR的中心,![]() 分别是OP、OQ、OR的中点,则△
分别是OP、OQ、OR的中点,则△![]() 与△PQR是位似三角形.此时,△
与△PQR是位似三角形.此时,△![]() 与△PQR的位似比、位似中心分别为
与△PQR的位似比、位似中心分别为
[ ]
(2)如图,用下面的方法可以画△AOB的内接等边三角形.阅读后证明相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;
②连结OE并延长,交AB于点![]() ,过点
,过点![]() 作
作![]() ∥EC,交OA于点
∥EC,交OA于点![]() ,作
,作![]() ∥ED,交OB于点
∥ED,交OB于点![]() ;
;
③连结![]() .则△
.则△![]() 是△AOB的内接三角形.
是△AOB的内接三角形.
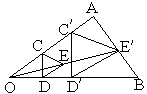
求证:△![]() 是等边三角形.
是等边三角形.
查看答案和解析>>
科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:047
| |||||||||||||||||||||
查看答案和解析>>
科目:初中数学 来源:2012年沪科版初中数学八年级上15.1全等三角形练习卷(解析版) 题型:选择题
如图, 与
与 都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“
都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“ ”可以表示为( )
”可以表示为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com