Question

【题目】如图1，地面BD上两根等长立柱AB，CD之间悬挂一根近似成抛物线的绳子．

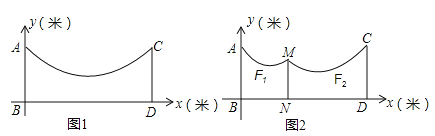
（1）求绳子最低点离地面的距离；

（2）因实际需要，在离AB为3米的位置处用一根立柱MN撑起绳子（如图2），使左边抛物线F1的最低点距MN为1米，离地面1.8米，求MN的长；

（3）将立柱MN的长度提升为3米，通过调整MN的位置，使抛物线F2对应函数的二次项系数始终为，设MN离AB的距离为m，抛物线F2的顶点离地面距离为k，当2≤k≤2.5时，求m的取值范围．

Answer 1

【答案】（1）m；（2）2.1m；（3）4≤m≤．

【解析】

试题分析：（1）直接利用配方法求出二次函数最值得出答案；

（2）利用顶点式求出抛物线F1的解析式，进而得出x=3时，y的值，进而得出MN的长；

（3）根据题意得出抛物线F2的解析式，得出k的值，进而得出m的取值范围．

试题解析：（1）∵a=＞0，∴抛物线顶点为最低点，∵=，∴绳子最低点离地面的距离为：m；

（2）由（1）可知，BD=8，令x=0得y=3，∴A（0，3），C（8，3），由题意可得：抛物线F1的顶点坐标为：（2，1.8），设F1的解析式为：，将（0，3）代入得：4a+1.8=3，解得：a=0.3，∴抛物线F1为：，当x=3时，y=0.3×1+1.8=2.1，∴MN的长度为：2.1m；

（3）∵MN=DC=3，∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上，∴抛物线F2的顶点坐标为：（，k），∴抛物线F2的解析式为：，把C（8，3）代入得：，解得：，∴k=，∴k是关于m的二次函数，又∵由已知m＜8，在对称轴的左侧，∴k随m的增大而增大，∴当k=2时，，解得：，（不符合题意，舍去），当k=2.5时，，解得：，（不符合题意，舍去），∴m的取值范围是：4≤m≤．