
 ,求AE的长.
,求AE的长.
 与a+b=c+4,可求得a,b,c的值,又由平行线分线段成比例定理,可求得半径的长,继而求得答案.
与a+b=c+4,可求得a,b,c的值,又由平行线分线段成比例定理,可求得半径的长,继而求得答案.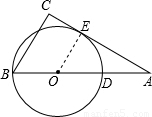 (2)∵∠C=90°,
(2)∵∠C=90°,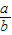 =
= ,
,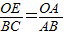 ,
,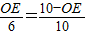 ,
, ,
,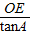 =
=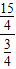 =5.
=5.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 某花木场有一块形如等腰梯形ABCD的空地(如图),各边中点分别为E、F、G、H,测得对角线AC=5m,若用篱笆围成四边形EFGH的场地,则需篱笆总长度为
某花木场有一块形如等腰梯形ABCD的空地(如图),各边中点分别为E、F、G、H,测得对角线AC=5m,若用篱笆围成四边形EFGH的场地,则需篱笆总长度为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com