
如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD
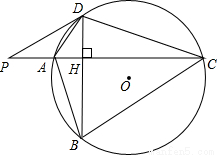
(1) 试判断PD与⊙O的位置关系,并说明理由
(2) 若tan∠ADB=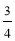 ,PA=
,PA=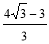 AH,求BD的长
AH,求BD的长
科目:初中数学 来源:2016届江苏省泰兴市九年级下学期第一次知识质量调查数学试卷(解析版) 题型:解答题
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=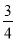 x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
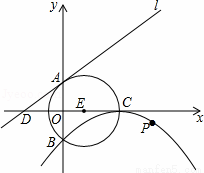
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
查看答案和解析>>
科目:初中数学 来源:2016届湖北省武汉市九年级下3月考数学试卷(解析版) 题型:填空题
我们把a、b中较小的数记作min{a,b},设函数f (x)={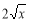 ,|x-2|}.若动直线y=m与函数y=f (x)的图象有三个交点,它们的横坐标分别为x1、x2、x3,则x1x2x3的最大值为_________
,|x-2|}.若动直线y=m与函数y=f (x)的图象有三个交点,它们的横坐标分别为x1、x2、x3,则x1x2x3的最大值为_________
查看答案和解析>>
科目:初中数学 来源:2016届湖北省武汉市九年级下3月考数学试卷(解析版) 题型:选择题
如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,……,如此继续,可以依次得到点D4、D5、……、Dn,分别记△BD1E1、△BD2E2、△BD3E3、……、△BDnEn的面积为S1、S2、S3,……Sn,则( )
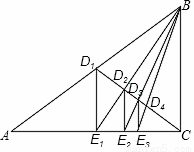
A. B.
B.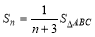 C.
C.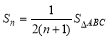 D.
D.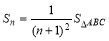
查看答案和解析>>
科目:初中数学 来源:2016届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
阅读材料:如图(一),△ABC的周长为 ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积

∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB= ,S△OBC=
,S△OBC= ,S△OCA =
,S△OCA =
∴S△ABC= +
+ +
+ =
= (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com